フィードバックの概要
ブロックダイアグラム
一般に、フィードバック系は Fig.1-1a のようなブロック線図で表されます。
ここで、 は入力で、 は出力、 は Open Loop の入出力伝達関数で、 はフィードバックの伝達関数を表します。
複号が正の場合を「正帰還」、負の場合を「負帰還」と呼び、一般には負帰還が使われます。
さらに、フィードバックの伝達関数としては、s を含まない定数(フィードバック係数)を用いることが多いです。
それを考慮すると、Fig.1-1b のブロック線図が得られますので、この図を元に入出力の関係を求めます。
における入力を とすると出力 は、
入力を からフィードバック分の を減じた分が なので、
これを について整理すると、
だから、
以上から、入力に対する出力の伝達関数は、
したがってこの 係数 でフィードバックをかけたときの Closed Loop 特性は、Fig.1-1c に示すブロック線図と等価になります。
なお、ここでフィードバックで戻ってくる分をループゲインと呼び、Closed Loop 特性を決める重要なパラメータになります。
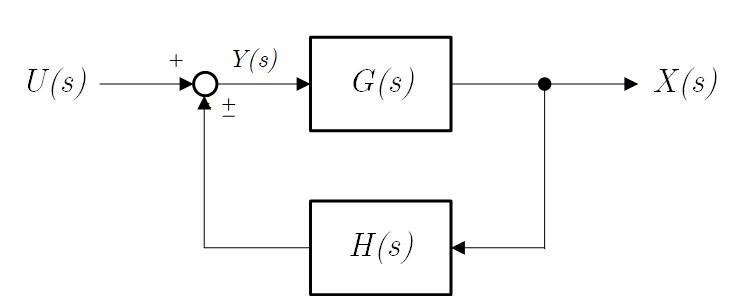
Fig.1-1a
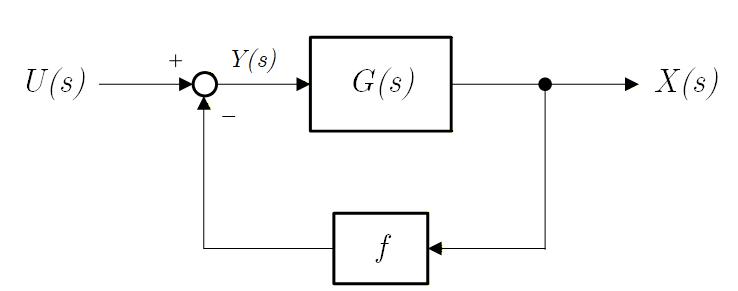
Fig.1-1b
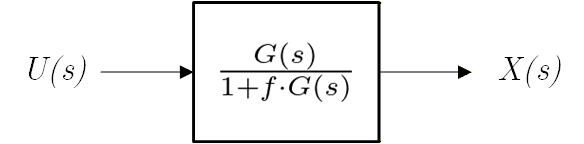
Fig.1-1c
アナログ回路では、フィードバック回路というと負帰還が使われることがほとんどですが、例外として発振回路やラッチ型コンパレータなどで正帰還で使われます。
オペアンプを使った回路例
いま仮に を を含まない単純な 入力を 倍するだけの伝達関数と仮定するとブロック線図は Fig.1-2a のようになります。
前節で求めた Closed Loop の伝達関数を計算すると以下のようになります。
いま、 とすると
と、フィードバック係数の逆数に等しくなることがわかります。
このことは、十分大きなゲインを持つアンプでフィードバックをかけると、Closed Loop ゲインは Open Loop ゲインによらず、 という一定の値となることを意味します。
これを実際のアンプを使った非反転増幅回路(Fig.1-2b)と比較してみます。
周知のように、 とすると
です。
これをブロック線図と比較してみると、 の係数でフィードバックをかけたものと等価であり、Closed Loop の入出力ゲイン比さは、
と、両者は等しくなることがわかります。
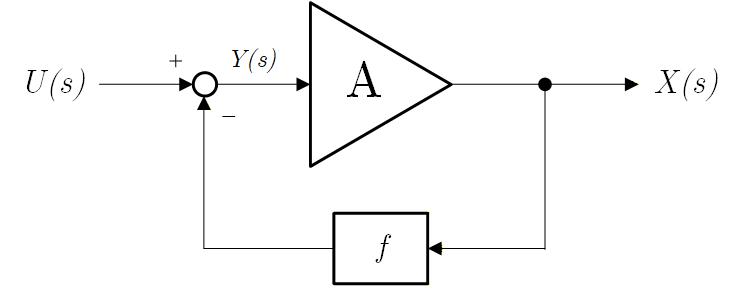
Fig.1-2a
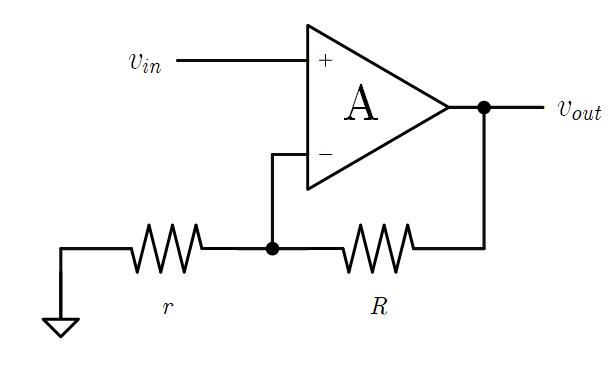
Fig.1-2b
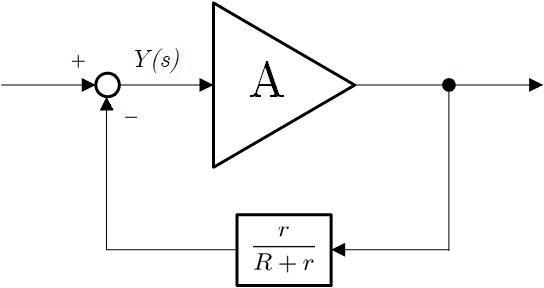
Fig.1-2c
フィードバックの効果
フィードバックの効果として代表的なものには以下の4つが挙げられます。
① ゲイン変動が小さい
② ひずみが小さい
③ 出力インピーダンスが下がる
④ 動作帯域が向上する
以下、それぞれについて説明していきます。
ゲイン変動が小さい
前節で説明しましたが、Fig.2-1 のように Open Loop ゲインが のアンプを用いてフィードバック係数 で帰還をかけた場合の入出力ゲインは、
で与えられ、 が大きくなると入出力ゲインは に近きます。
更に変形すると、
となって、ゲイン誤差としてはループゲイン の逆数として与えられることになります。
例えば、 の全帰還をかけたときには、 の値によってゲイン誤差は以下のようになります。
→ 1%
→ 0.1%
→ 0.01%
用途にもよりますが、60dB 以上の Open Loop ゲインを持つアンプを使ってフィードバックをかけると、 Closed Loop ゲインはほとんど誤差なく、フィードバック係数のみでゲインが決定されます。
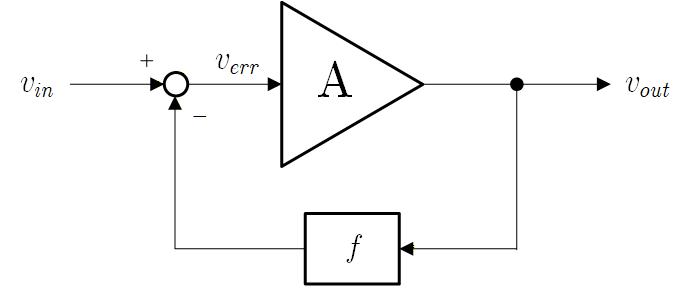
Fig.2-1
「アナログ回路の基本要素」 の章でアンプのゲインは大きい方がよいと述べたのは、アンプではフィードバックをかけて使うという前提があるためです。 アンプの Open Loop ゲインは , で決まるため、動作点や電源電圧・プロセス変動などがあると変動しますが、例えばそれが 60dB から 54dB と半減しても、Closed Loop でのゲイン誤差が 0.1% → 0.2% となる程度の影響しか及ぼしません。
ひずみが小さい
まず、前章で説明した抵抗負荷のインバータ (Fig.2-2a ) に対して、小信号ではなく 入力振幅がある程度大きな “大信号” 入力を与えたた場合について考えます。
この時抵抗負荷のインバーターの入出力特性は線形な応答にはなりません。 これはトランジスタの動作領域が 3極管領域に入るなどして、 や が一定ではなくなり、ゲインが動作点によって変化するためです。
このため入力に正弦波を入力したとしてもその出力は曲がった入出力特性で変換されるため 出力は歪むことになります。(Fig.2-2b )
これに対してフィードバックをかけたアンプを使用した場合、その Open Loop ゲインが動作点によって変化したとしても、それが十分大きければ入出力ゲインはフィードバック係数のみで決まるため、動作範囲において入出力特性はゲイン一定の直線になります。
Open Loop ゲインが十分 大きければ Closed Loop のゲインはほぼ一定なので入出力特性が直線で近似できます。
このため入したに正弦波を正しくゲイン倍した歪のない出力が得られます。
(Fig.2-2c)
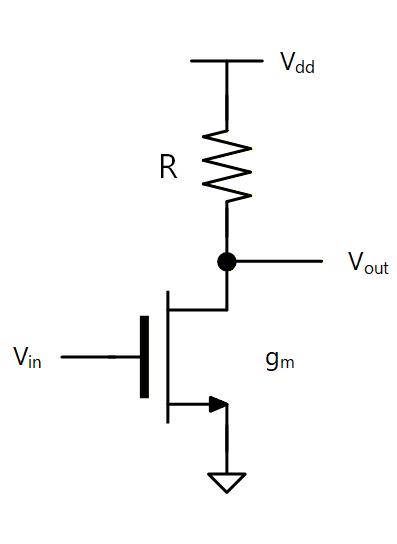
Fig.2-2a
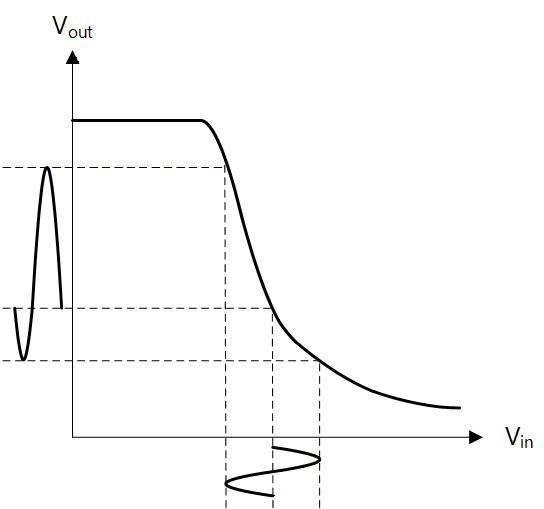
Fig.2-2b
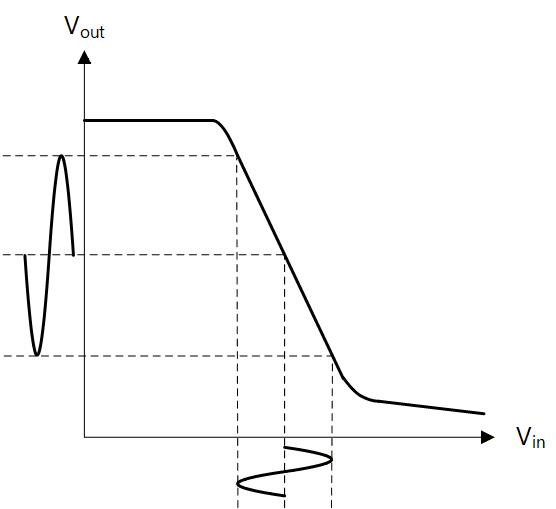
Fig.2-2c
出力インピーダンスが下がる
アンプは出力インピーダンスを持ちます。 これがフィードバックをかけることによって どのように変化するかを考えます。
Fig.2-3 に示すようにアンプを、入力の信号をゲイン倍した電圧源と出力抵抗として表します。
出力抵抗は、出力を開放きた時の電圧と、出力が短絡した時の電流の比で表すことができますので、それぞれを計算します。
①出力開放電圧
②出力短絡電流
出力が短絡されるため になるから
③出力インピーダンス
とすると
以上から、出力抵抗は元々のアンプの出力インピーダンスの をループゲイン分の1 にしたもの に等しくなります。
例えば、、 とすると、 と、非常に小さくすることが可能となります。
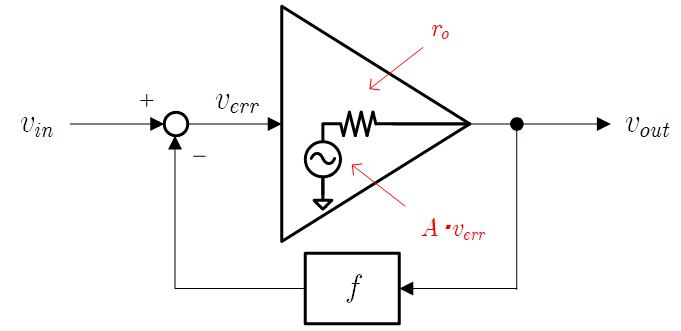
Fig.2-3
動作帯域が向上する
アンプの Open Loop での伝達関数を とし、DCゲインが で、角周波数が で単一の Pole を持つ一次遅れ応答を示すものと仮定します。
ここで、フィードバックをかけたときの入出力特性を計算します。
とすると、
以上から DCゲインはもとの Open Loop ゲインの に対して になり、代わりに Pole 角周波数は 倍になることがわかります。 つまり、フィードバックによってゲインを抑圧した分だけ帯域を向上させることが可能となります。
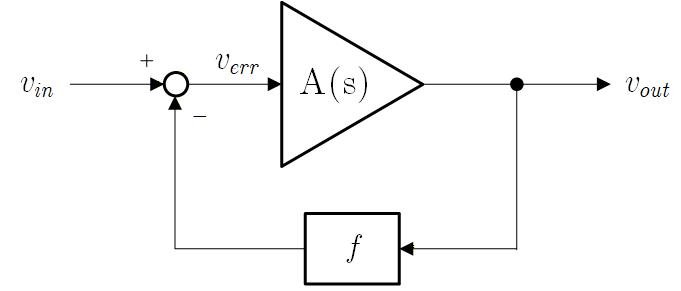
Fig.2-4
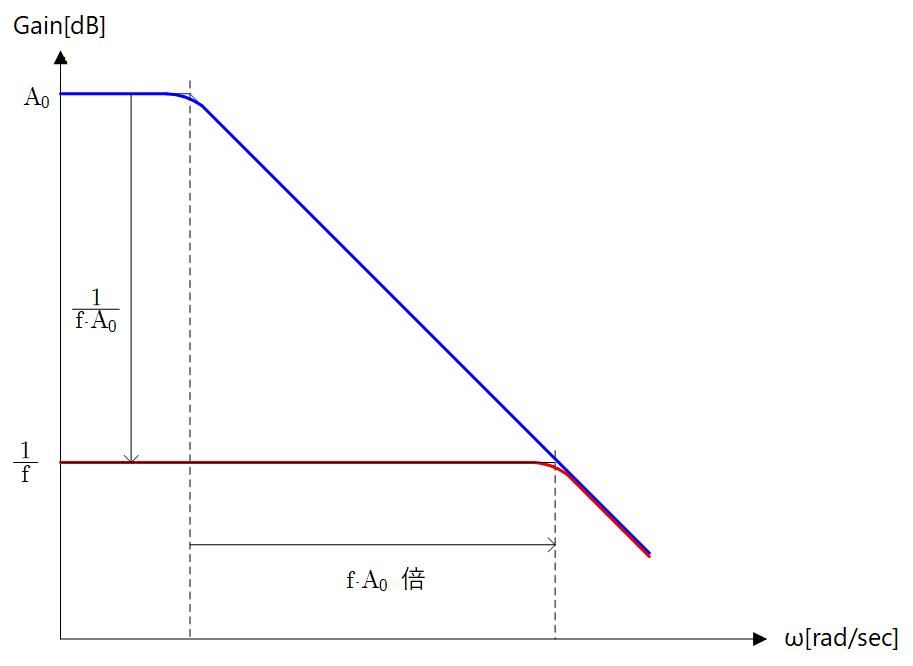
Fig.2-5
帯域幅とゲインをかけたものを GB積と呼び、アンプの性能の指標としてよく使われます。 (G は Gain 、B は Band Width の頭文字)
GB積は一定なので、常にゲインと帯域はトレードオフの関係にあります。 フィードバック係数を大きくしていくと帯域は向上しますがゲインは下がります。 逆にフィードバック係数を小さくしていくとゲインは高くなりますが帯域は稼げません。
フィードバックの安定判別
前節にてフィードバックの利点を説明してきましたが、良いことばかりではなく当然ながら欠点もあります。 フィードバックの欠点としては、条件によっては系が不安定になり、発散や発振という問題が発生する可能性があることが挙げられます。
この節ではフィードバックループを安定条件で使うための判別方法について説明します。
Closed Loop での安定判別
Open Loop の伝達関数が G(s) で表される回路に係数 f でフィードバックをかけた場合の伝達関数 は、
で表されます。 この伝達関数の分母=0 とした式を特性方程式と呼びます。
この特性方程式の根が Closed Loop の伝達関数の極(Pole) となり、この Pole が s 平面の左半面にあるか右半面にあるかで、安定性が決まります。
特性方程式 の根を p1, p2,…, pn とすると、 は、
と因数分解でき、 は、以下のように部分分数に展開できます。
これをラプラス逆変換すると、
p1, p2,…, pn の中で実部が負の項は収束しますが、正の項は発散します。 つまり特性方程式の根の中に実部が正の根がある場合、すなわち根が右半面にある場合には発散することになります。
以上から、Fig. 3-2a のように、特性方程式の根が左半面にのみあれば安定で、Fig.3-2b のように右半面に存在すれば不安定と判断できます。
Fig.3-1
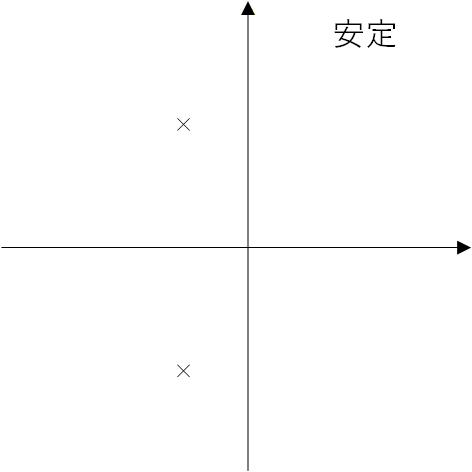
Fig.3-2a
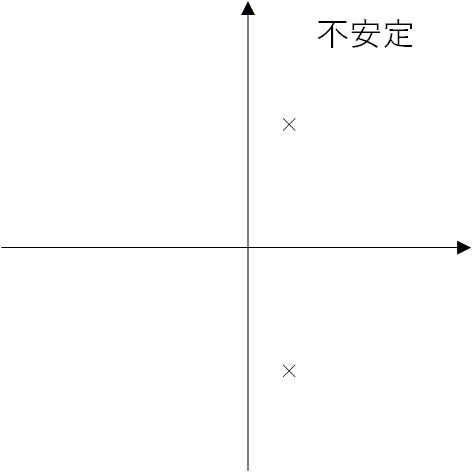
Fig.3-2b
以上、安定条件について説明してきましたが、根が左半面にあっても、それが虚軸に近い場合(Fig.3-3a) には、発散はしないものの不安定な状態に近づきます。 つまり安定マージンがないということです。
一方、根が虚軸から離れていれば (Fig.3-3b)、その系は安定マージンがあると判断できます。
以下、特性方程式が 2次の場合を例にとって説明します。
特性方程式の根を とおくと、ラプラス逆変換すると以下のように、減衰項と振動項の和になります。
特性方程式の根の実部 () は減衰の速さを示し、大きくなれば応答が速やかに収束することを意味します。
また根の虚部 () は振動の周波数を示し、大きくなれば高周波で振動することを意味します。
一般に振動項があっても速やかに減衰すれば問題はありませんし、逆に減衰項が小さいと振動がなかなか収まらないので、 と の比で安定度を判断するのが妥当です。
つまり、 が大きい方が安定マージンが充分あり、 が小さいと安定マージンが乏しいと判断します。
ここで、 とおくと、 は 0°〜90° の範囲になり、 が 0° に近いと安定で、90° に近づくと不安定になります。
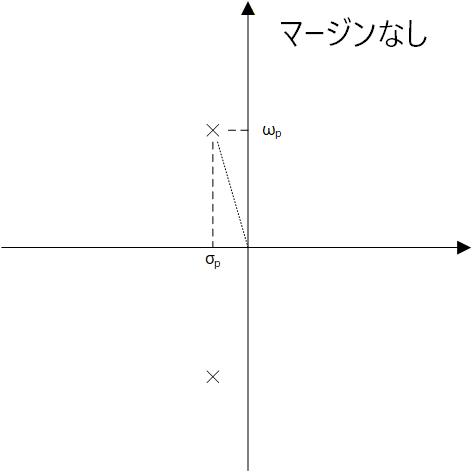
Fig.3-3a
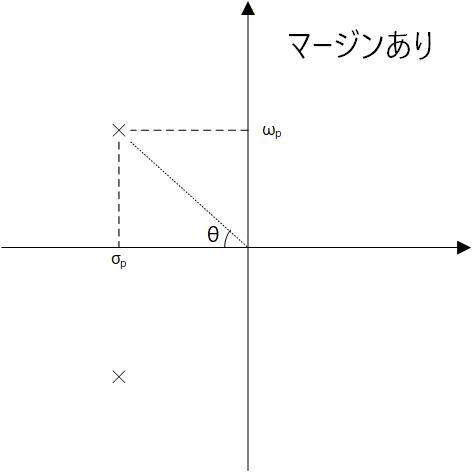
Fig.3-3b
特性方程式の根が実数の場合は振動項がなく望ましいように思えますが、若干振動した方が収束が早くなります。
といって を小さくしすぎても安定マージンを損ねるので、一般的には ° 程度を目標にすることが多いです。
ここで、「ラプラス変換の使い方」 で説明した、ダンピングファクター() と の関係について調べます。
ダンピングファクターを用いた場合の特性方程式は次式で与えられます。
特性方程式が虚根を持つ場合は、根は以下の共役複素数となります。
根の実部を と虚部を としてその比を取ると、
ここで とおくと、 の関係が得られます。
° が に相当し、° が となります。 また、° は に相当します。
続いて、Fig.3-4a〜Fig.3-4e に、2次の場合についてダンピングファクターを変化させたときの周波数特性のグラフを示します。
では特性方程式が実根を持ち、ゲインは周波数とともにダラダラ落ちるように振る舞い、いわゆるカットオフ周波数に達する以前にゲインが落ち始めていることから、入力信号に対する応答が遅いことがわかります。
では特性方程式は重根を持ち、カットオフ周波数近辺でのゲインの落ち方は多少緩和されますが、依然として残っています。
になると特性方程式は虚根を持つために振動項が現れますが、周波数応答的にはカットオフ周波数までゲインは 0dB を維持し、良好な特性が得られていることがわかります。
になると、カットオフ周波数の手前でピーキングを持つのが見えます。
すなわち、入力信号に対して本来等倍のゲインしか持たないはずが、むしろ増幅するように振る舞います。
までいくとピーキングはさらに顕著になり、グラフではカットオフ周波数で約 10dB (=約3倍) のゲインが出ています。
これはもし 関数 やステップ関数のように信号があらゆる周波数成分を均等に含む白色だったとしても、カットオフ周波数近傍の成分のみが増幅されるため、トランジェントでみるとその周波数のリンギングが観測されることになります。
このように、特性方程式の根が右半面に入らなくても、 に近づくすなわち根が右半面に近づくと、応答が振動気味になって不安定になることがわかります。
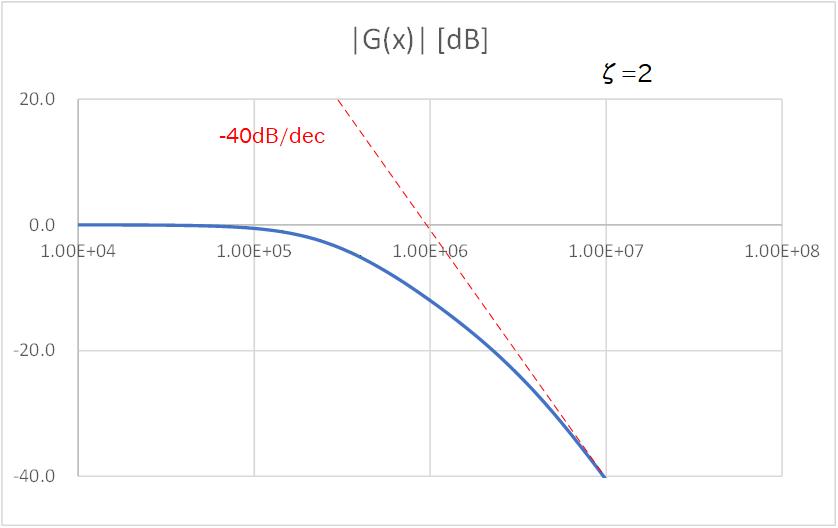
Fig. 3-4a
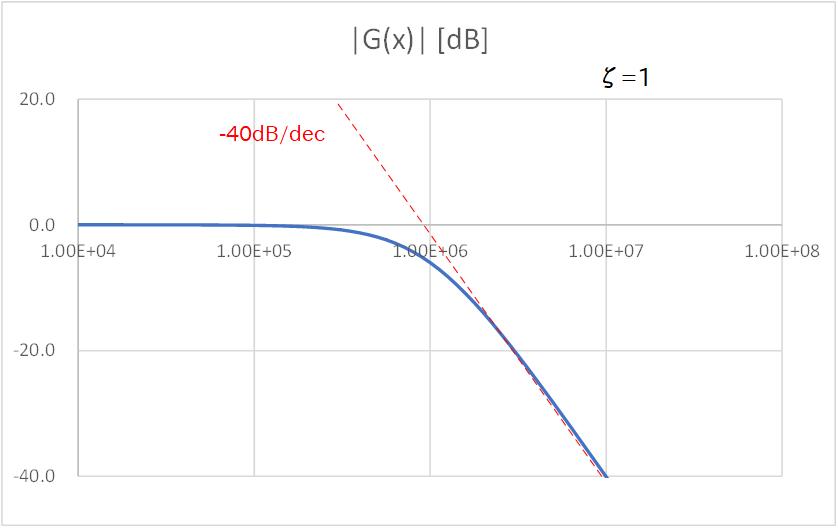
Fig. 3-4b
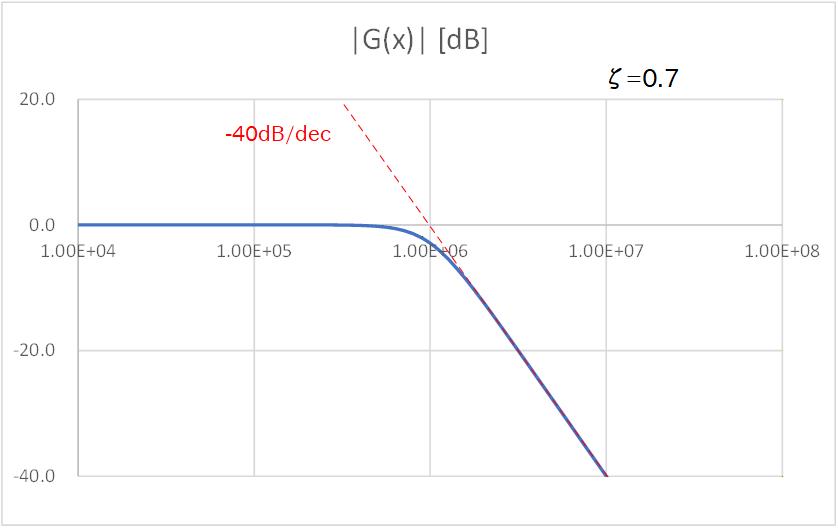
Fig. 3-4c
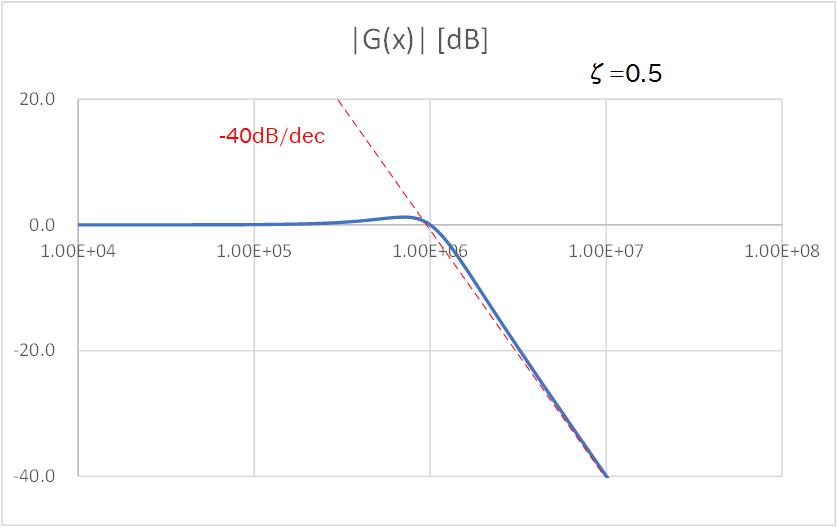
Fig. 3-4d
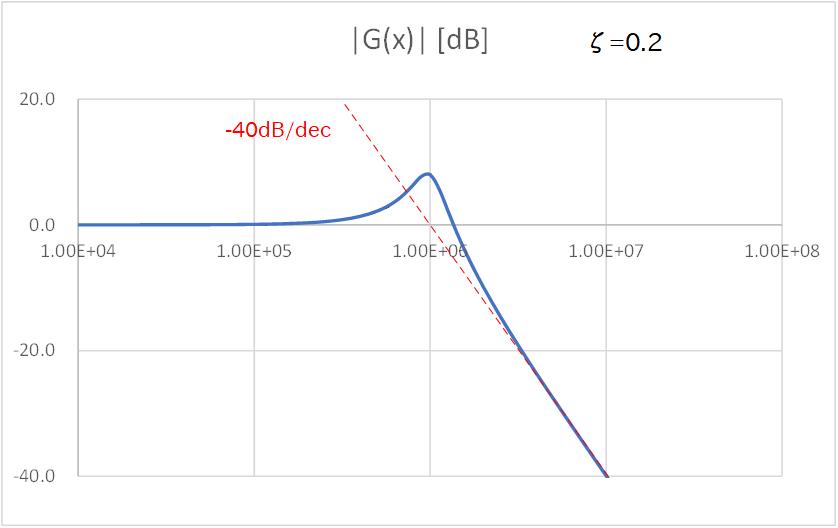
Fig. 3-4e
根軌跡
アンプは通常はゲインを稼ぐために何段かの増幅回路をカスケード接続して構成します。(Fig. 3-5a)
各増幅回路はそれぞれ時定数 の 1次遅れ要素なので、トータルでの伝達関数はそれらの積として表されます。
とおくと、
特性方程式は
ここで、 は正の実数なので特性方程式の根は左半面にしか出ません。
次に Fig. 3-5b のように 係数 でフィードバックをかけた場合を考えます。
この場合の特性方程式は、
と表されます。
の場合は Open Loop と変わらないので、根は全て左半面にありますが、 を大きくしていくと右半面に根が入ってくる可能性があります。
をゼロから徐々に大きくして 行った場合の特性方程式の根の軌跡を s平面上に描いたもを根軌跡と呼び、根が右半面にはいるかどうかで安定判別ができます。 つまり を大きくしていって根が右半面に入ったら、そのフィードバック系は不安定になるということです。
以下、特性方程式が 1次の場合、2次の場合、3次の場合のそれぞれについて、根軌跡をみていきます。
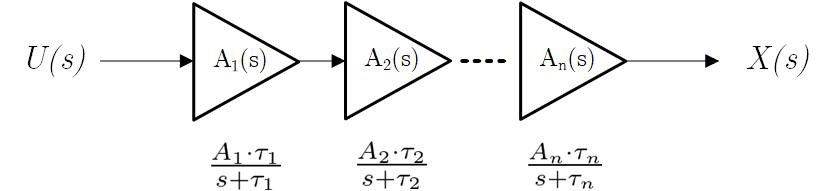
Fig.3-5a
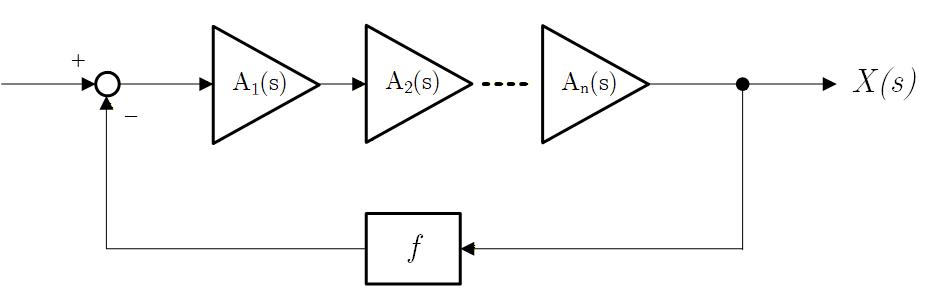
Fig.3-5b
一次の場合の根軌跡
Open Loop の伝達関数は以下で表されます。
特性方程式は、
これを解くと、
となり、もとの Pole である が 倍された位置に移動して行きます。
(Fig.3-6a)
この時 , はどちらも実数なので特性方程式の根は とともに実軸上を高周波側 (負側) に動くだけなので、右半面には絶対に現れず、確実に安定であるといえます。
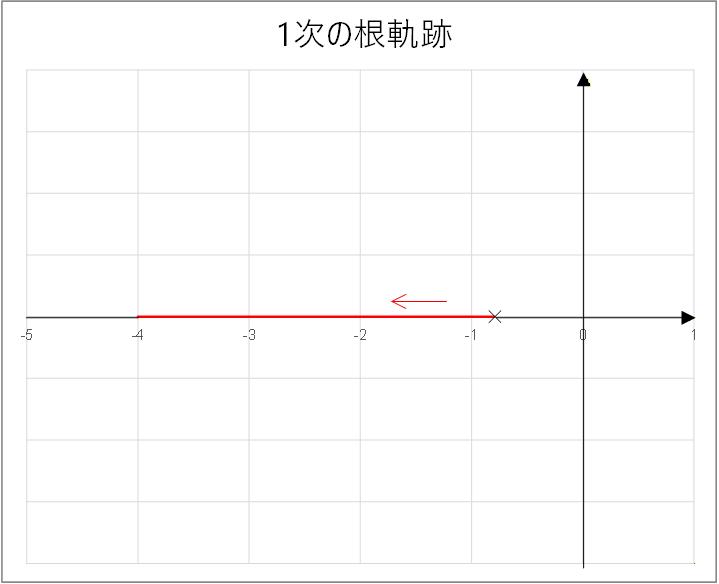
Fig.3-6a
ニ次の場合の根軌跡
OpenLoop の伝達関数は以下で表されます。
特性方程式は、
この根軌跡を Fig.3-6b に示します。
根は の時点では実軸上の と にあり、 を大きくしていくと2つの根は近づき、やがて 1点に重なります。(重根)
更に を大きくしていくと根は2つの共役複素数となって実軸を離れます。
この時根の実部は変化せず、虚部のみが大きくなって行きます。
虚部と実部の比はどんどん大きくなり、減衰項より振動項が支配的になっていきますが、右半面に行くことはありません。
なので、とりあえず発散はしないことがわかります。
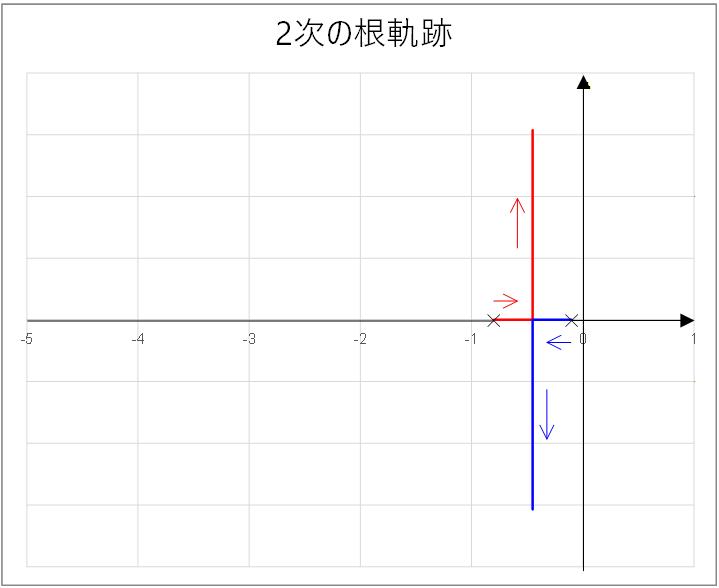
Fig.3-6b
三次の場合の根軌跡
OpenLoop の伝達関数は以下で表されます。
特性方程式は、
すなわち
この根軌跡を Fig.3-6c に示します。
根は の時点では実軸上の , および にあり、 を大きくしていくと 最も高周波の根は実軸上をさらに高周波側に動いて行きます。
低周波側の 2つの根は、2次の場合と似た動きをし、互いに近づいて重根となった後に実軸上を離れます。
2次の場合との違いは、 が大きくなっていくと 実部が小さくなることです。つまり根がどんどん右半面に近づき、ある から右半面に入ってしまうことがわかります。
つまり 3次の場合にはフィードバック係数次第では発散する可能性があることになります。
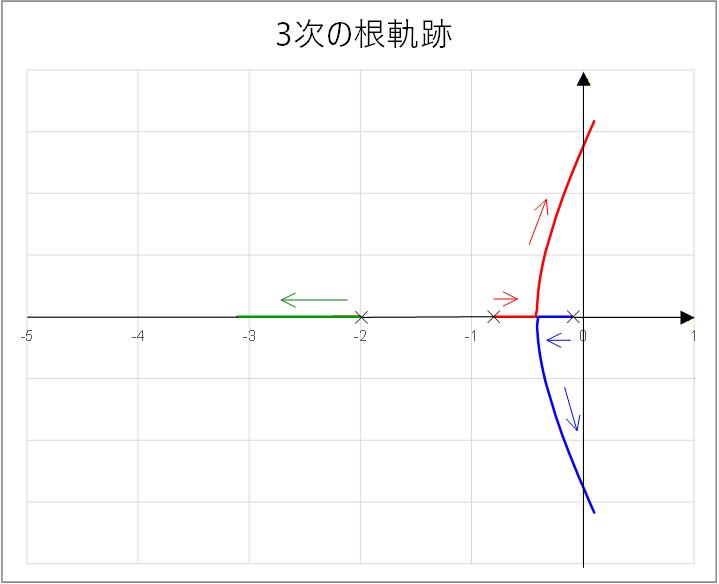
Fig.3-6c
Open Loop での安定判別
フィードバック系の安定判別のため、いちいち伝達関数を求めて、特性方程式の根の位置を確認するのは手間がかかります。
実は Open Loop の伝達関数とフィードバック係数、すなわち ループゲインから算出する方法が一般的です。 ここではその方法について説明します。
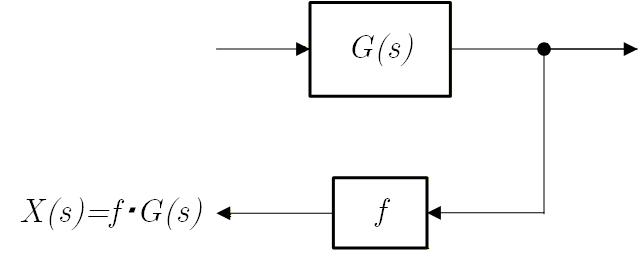
Fig. 3-7
ナイキストの方法
「ラプラス変換の使い方」 でも説明しましたが、ナイキスト線図とは Open Loop の伝達関数 の周波数特性、すなわち について、横軸に実数部、縦軸の虚数部をとり、 を媒介変数として から までの軌跡を描いたものになります。
(Fig.3-8)
ここで、軌跡が (-1, 0j) の点を巻き込めば不安定、巻き込まなければ安定と判定されます。
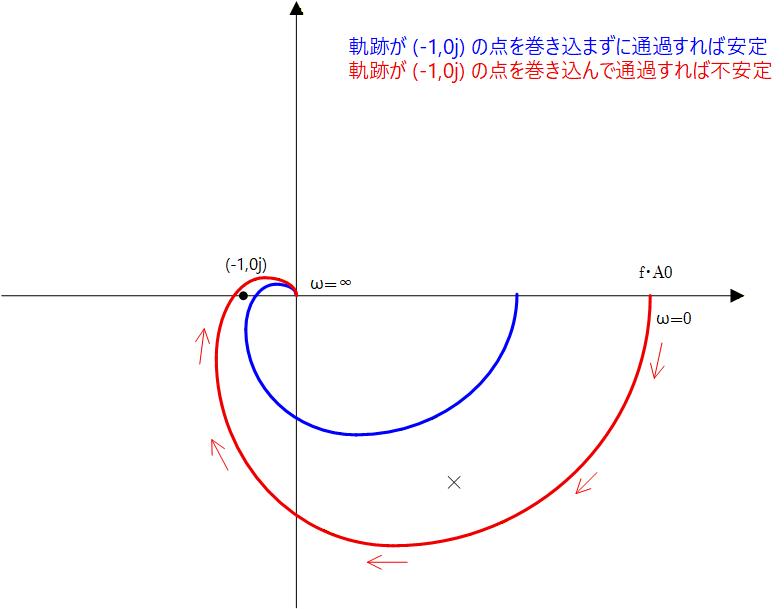
Fig. 3-8
Fig.3-9a 〜 Fig.3-9c に、それぞれ 1次、2次、3次の場合のナイキスト線図を示します。
図から明らかなように 1次、2次では (-1,j0) 点を巻き込むことはありません。
巻き込む可能性があるのは 3次以上の高次の場合のみです。
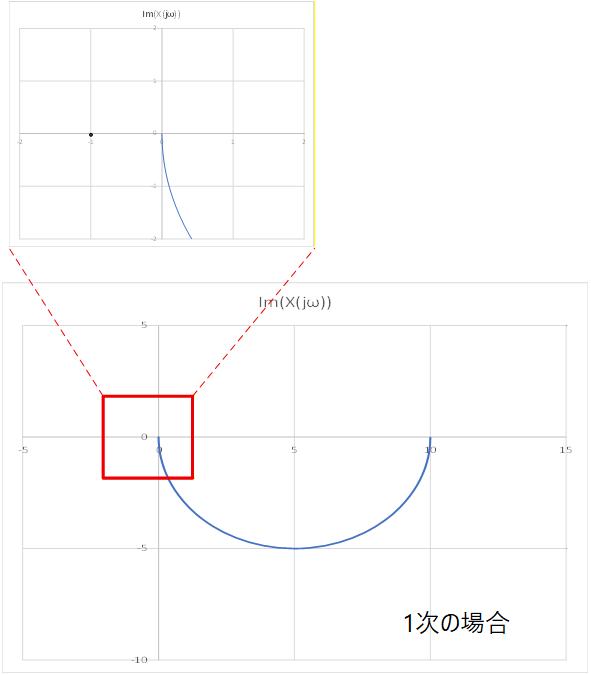
Fig.3-9a
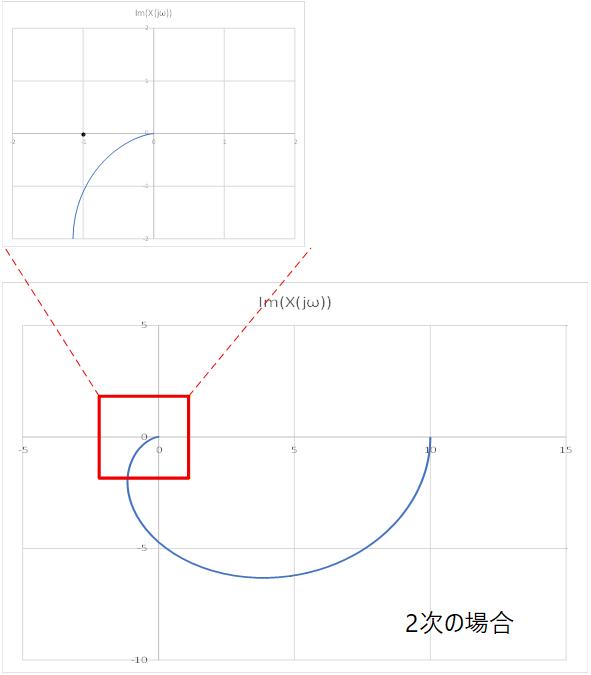
Fig.3-9b
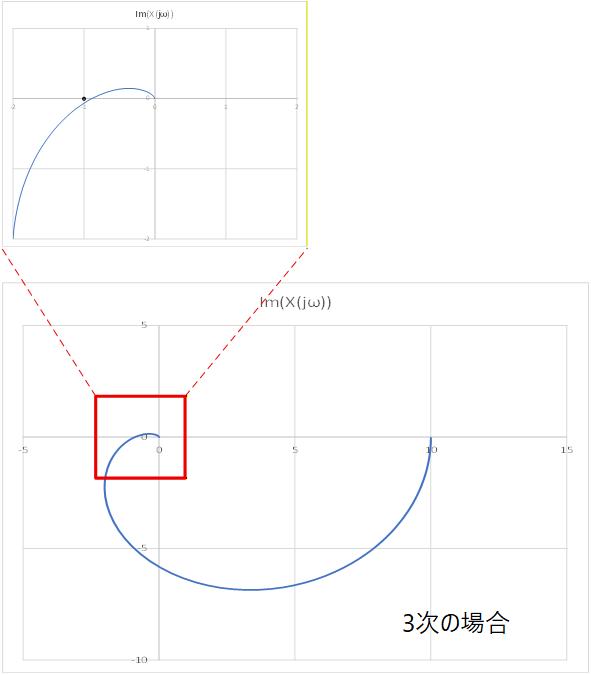
Fig.3-9c
2次以下の場合は (-1,j0) の点を巻き込むことはないので安定と述べましたが、 (-1,j0) の点を巻き込まなかったとしても、やはりギリギリだった場合には安定マージンが乏しくなり、応答が減衰項よりも振動項が支配的になって、振動がなかなか収まらないという振る舞いになります。
このため、 Fig.3-10 のように、
①ゲイン余裕
②位相余裕
で定義し、この余裕をなるべく確保するようにします。
位相余裕はゲインが 1、すなわち 0dB になったときに、位相が 180°に対してどれだけ余裕があるかを示した指標です。
また、ゲイン余裕は位相が 180°回ったときに、ゲインが 0dB よりどれだけ下がっているかを示す指標です。
一般的には位相余裕の方が重視され、その値としては 45°〜60° 以上が目安で、ゲイン余裕については、10〜20dB 以上というのが目安になります。
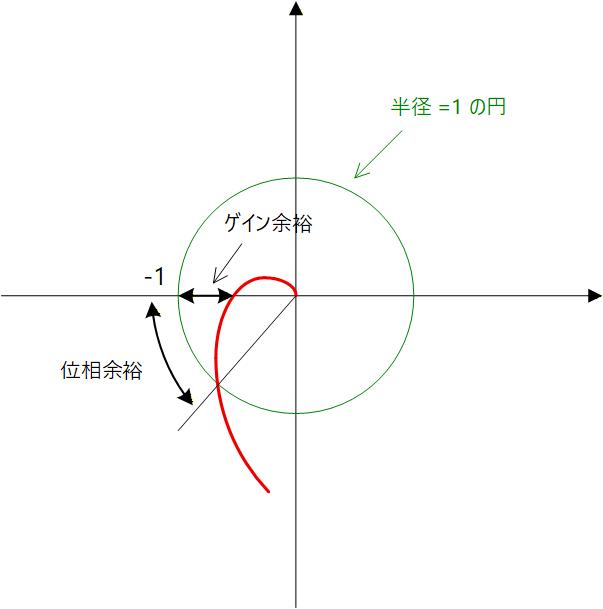
Fig.3-10
ナイキストの判定法の妥当性につきましては、Appendix で解説します。
ボード線図による方法
ナイキスト線図だと が明示的に現れないため、ボード線図による判定が多く使われます。
ボード線図とは「ラプラス変換の使い方」でも述べた通り、(角)周波数に対するゲイン (振幅) と、位相の関係をそれぞれ個別に表したものになります。
ボード線図の場合、角周波数 vs ゲインのグラフと、角周波数 vs 位相のグラフは、角周波数のスケールを同じにすることで、所定の角周波数の時のゲインと位相の関係が掴みやすくなります。
位相余裕はゲインが 0dB のときの位相を読めば出てきますし、ゲイン余裕は位相が 180° になったときのゲインを読めば出てきます。
なお、ゲインが 0dB となったときの周波数を Unity Gain 周波数と呼び、これがほとんどの場合 GB積に等しくなります。
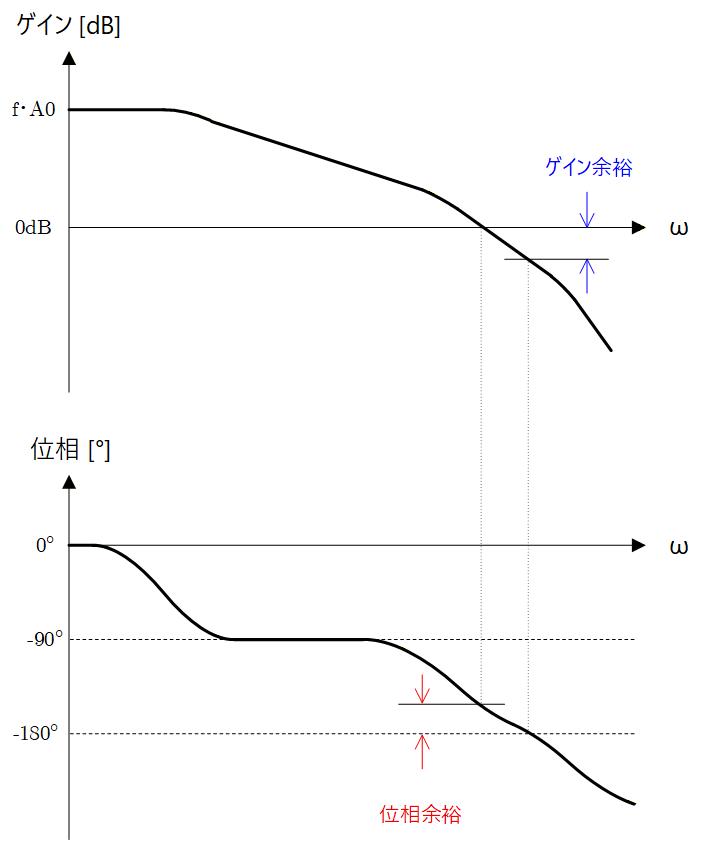
Fig.3-11
Fig.3-12a 〜 Fig.3-12c に、それぞれ 1次、2次、3次の場合のボード線図を示します。
それぞれ低周波から角周波数をスイープしていくと、オープンループゲインの伝達関数の極(Pole) を迎えるとゲインのグラフは折れ曲がり、傾きが 20dB/dec で減衰するようになり、さらに次の極(Pole) を迎えると 40dB/dec で減衰します。
位相については Pole 周波数を迎える度に位相がどんどん遅れて行き、では、1次の場合は -90° 、2次の場合は -180°、3次の場合には -270° に落ち着きます。
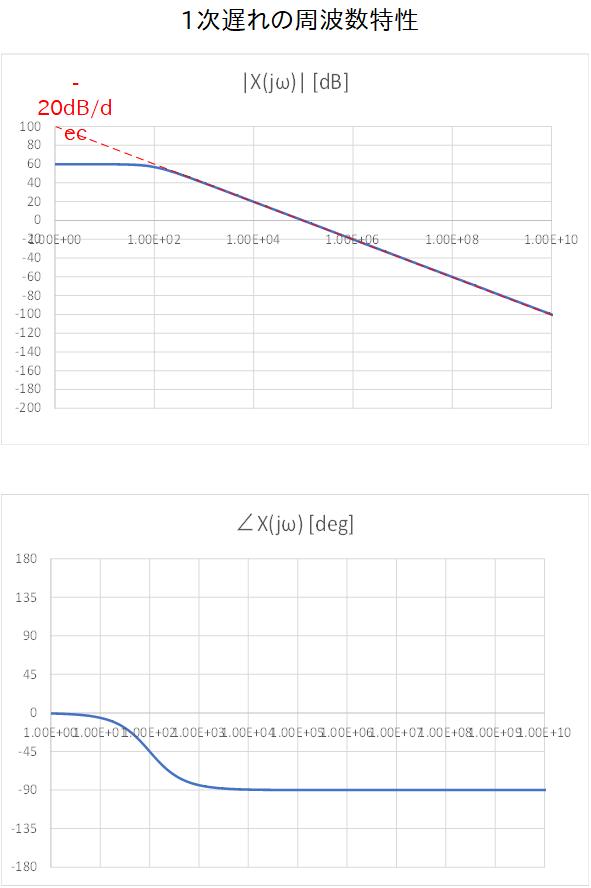
Fig.3-12a
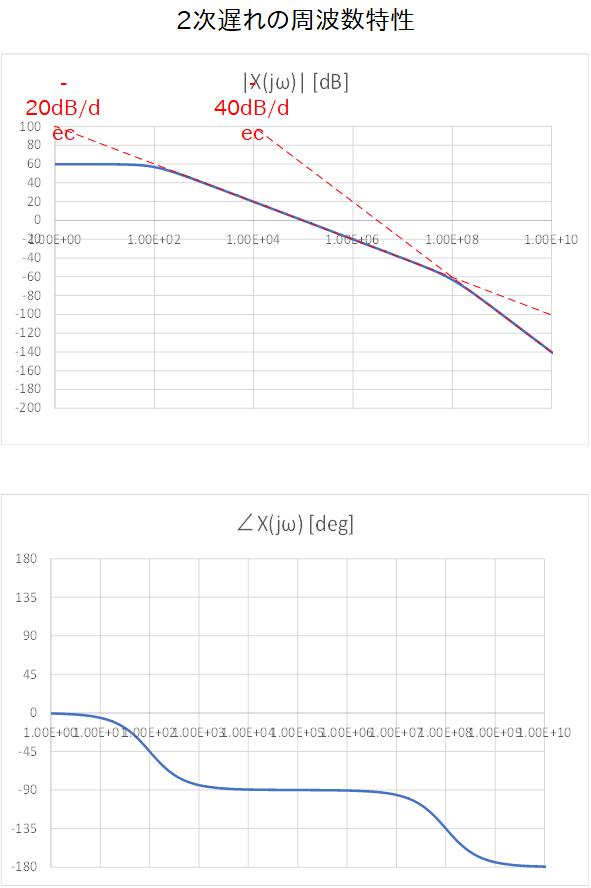
Fig.3-12b
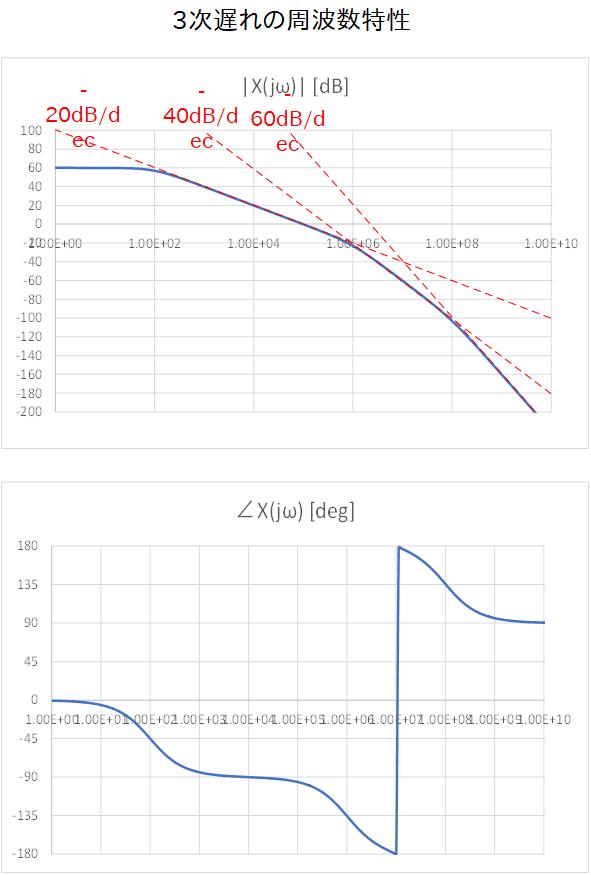
Fig.3-12c
まとめ
根軌跡から明らかなように、フィードバック係数を大きくすると不安定な方向に近づきますが、そうは言ってもフィードバック係数は Closed Loop の入出力ゲインを決めているので、変えられないことがほとんどです。 またアンプの Open Loop のゲインを小さくすると安定性の面では有利に働きますが、フィードバックの恩恵が小さくなってしまいます。
ですので、高いループゲインを維持したまま安定マージンを稼ぐために “位相補償” と呼ばれるテクニックを使います。
これについては次の 「オペアンプ」の章で解説します。
Appendix
ナイキストの判定法は、OpenLoop の周波数特性 において、 を 0 から∞まで変化させたときの軌跡が、 (-1,j0) の点を囲めば不安定・囲まなければ安定というものですが、ここではそれで判定できる根拠を示して行きたいと思います。
Open Loop の伝達関数を とすると
Closed Loop の伝達関数 は、
の分母の が特性方程式なので、これを満たす は、これが分母になる の Pole でもあり、 の Zero でもあります。
の Pole が右半面にあると系は不安定ということは、言い換えると の Zero が右半面にあると不安定ということになります。
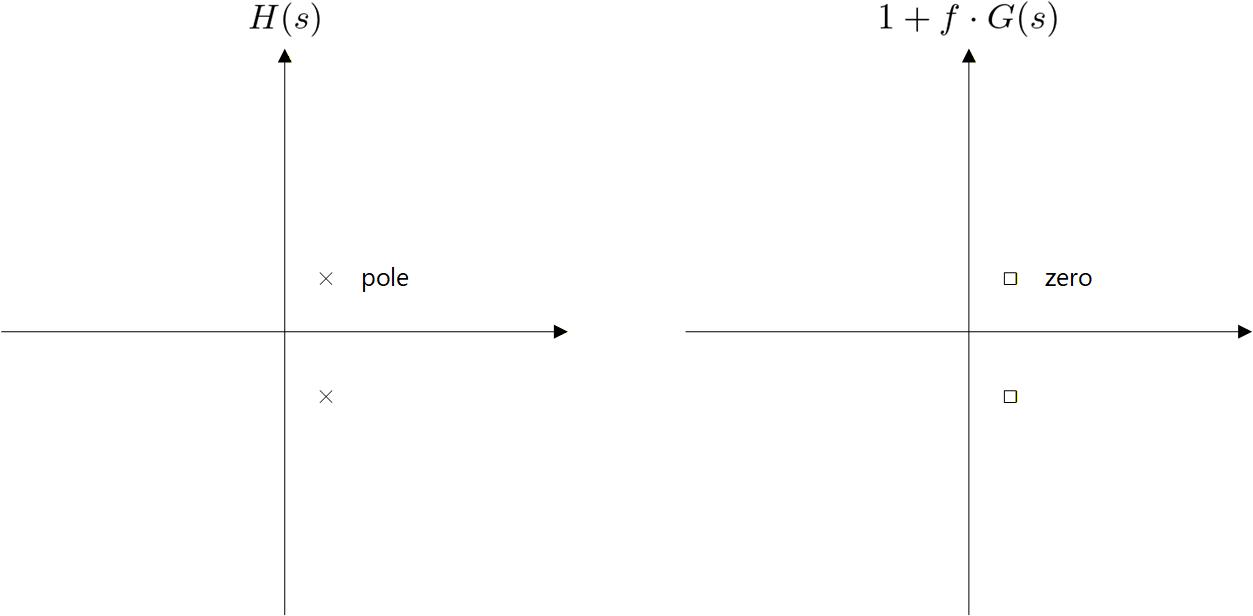
Fig. A-1
コーシーの偏角の原理から、 が、閉じた経路 CS 上で を動かすとき、 の軌跡 (CF) が原点を囲む回数 は、 の経路 CS で囲まれる領域内の Pole の数 から Zero の数 を引いたものに等しくなります。
の右半面での Pole の数 は、 の右半面での Pole の数 と同じ※ で、一般的に Open Loop では は右半面 に Pole は持たないので になります。
したがって、
となり、 であれば となって、 の右半面には Zero はなく、Closed Loop は安定であるということになります。
※ とすると、
なので、分母は同じ
なので Pole の数も同じ
すなわち、 が右半面で Zero を持つかどうかは、原点から の軌跡 (CF) へ引いたベクトルの位相が回転するかどうかで判定できます。
位相が回転しなければ Zero はなく安定で、位相が回転したらたら Zero があるので不安定です。
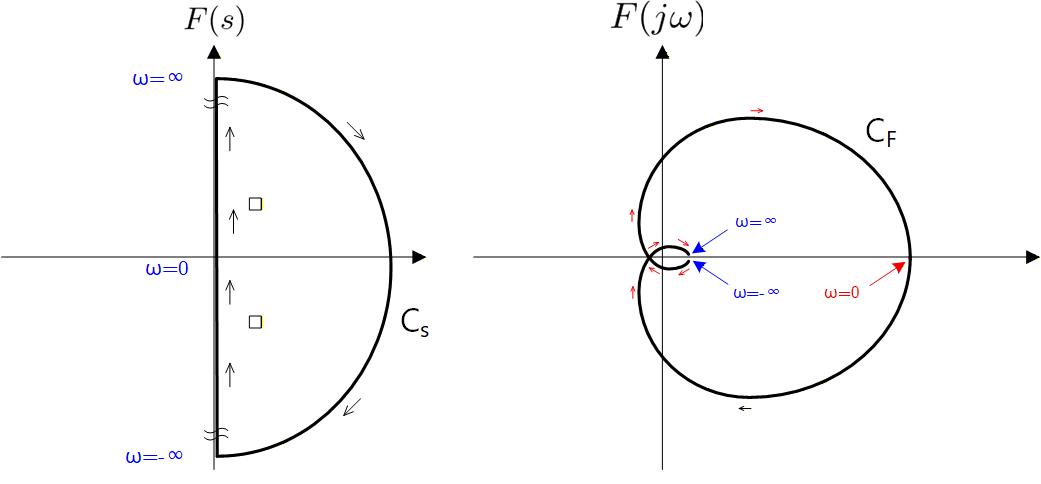
Fig. A-2
の軌跡 CF が原点を囲んでいれば、原点から軌跡 CF へ引いたベクトルは、
から へと動くと位相が 1回転し、 から へと動くとさらに 1回転するので合計2回転します。
(Fig. A-3 左)
一方、軌跡 CF が原点を囲まなければ、原点から軌跡 CF へ引いたベクトルは、 から へと動いても位相は回転しません。
(Fig. A-3 右)
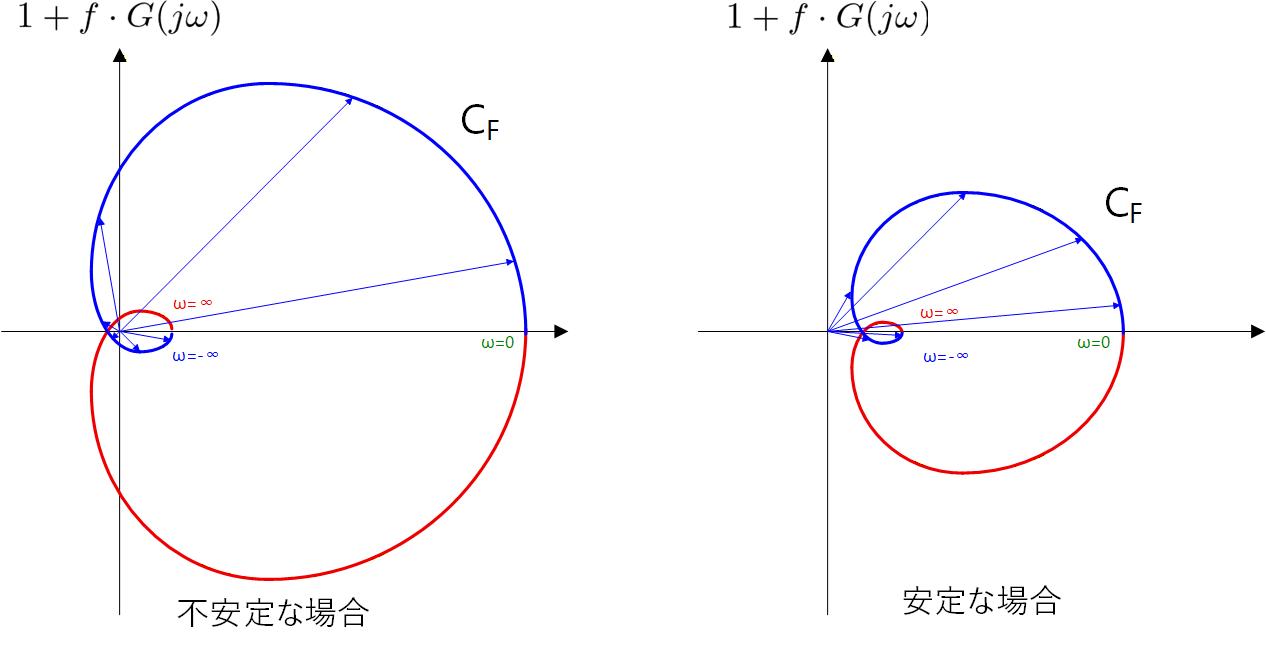
Fig. A-3
の軌跡を -1 だけ平行移動した軌跡が ナイキスト線図になるので、ナイキスト線図が (-1, j0) を囲まなければ安定で、囲んだら不安定ということになります。
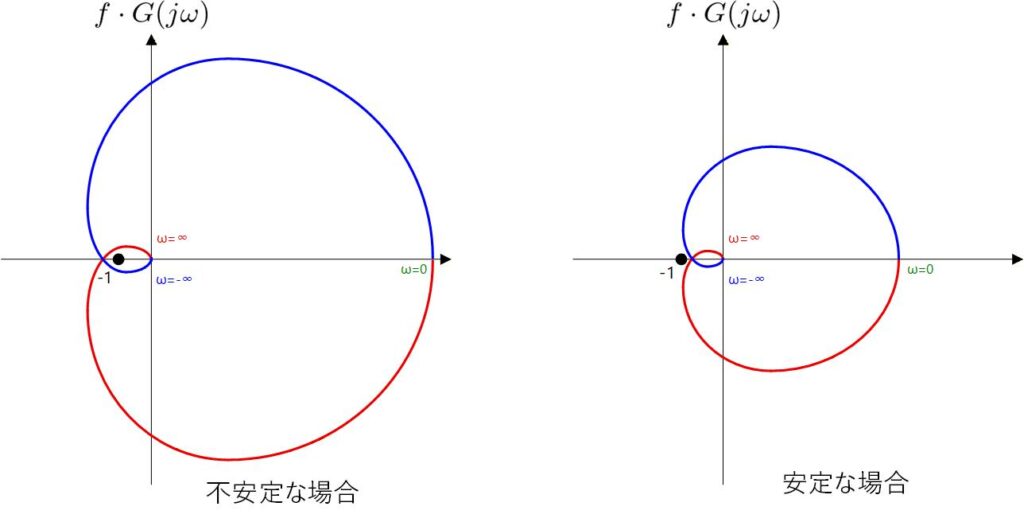
Fig. A-4



コメント