なぜラプラス変換なのか
ラプラス変換の定義
ラプラス変換の定義式は
ラプラス逆変換の定義式の定義式は
導関数のラプラス変換は
ラプラス変換では、時刻は t > 0 の範囲だけで考え、t = 0 における初期値は 0 を前提としているため結局
同様に積分については
以上のように、時間領域における微分・積分が ラプラス領域では s の乗算・除算で置き換えることができるため、複雑な微分方程式を単純な s についての代数方程式として表すことが可能となり、解くことが容易となります。
目次に戻る
ラプラス変換の使い方
ラプラス変換の一般的な使い方としては、t 領域の微分方程式をラプラス変換して s 領域の代数方程式に変換し、それを解いた後にラプラス逆変換して t 領域の解に戻します。
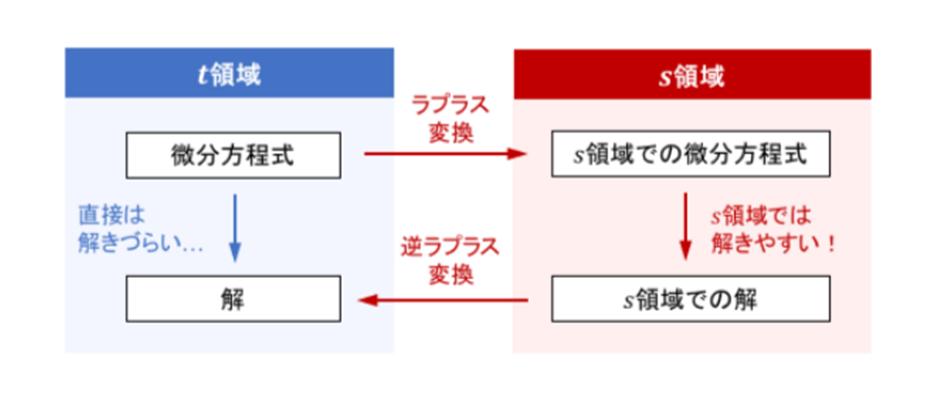
Fig. 1-1
※ https://controlabo.com/laplace-transform/
一見すると、回り道をするように見えるのですが、ラプラス変換・逆変換は右の変換表を使って機械的に行いますので、複微分方程式を解くよりも遥かにラクに解くことができます。
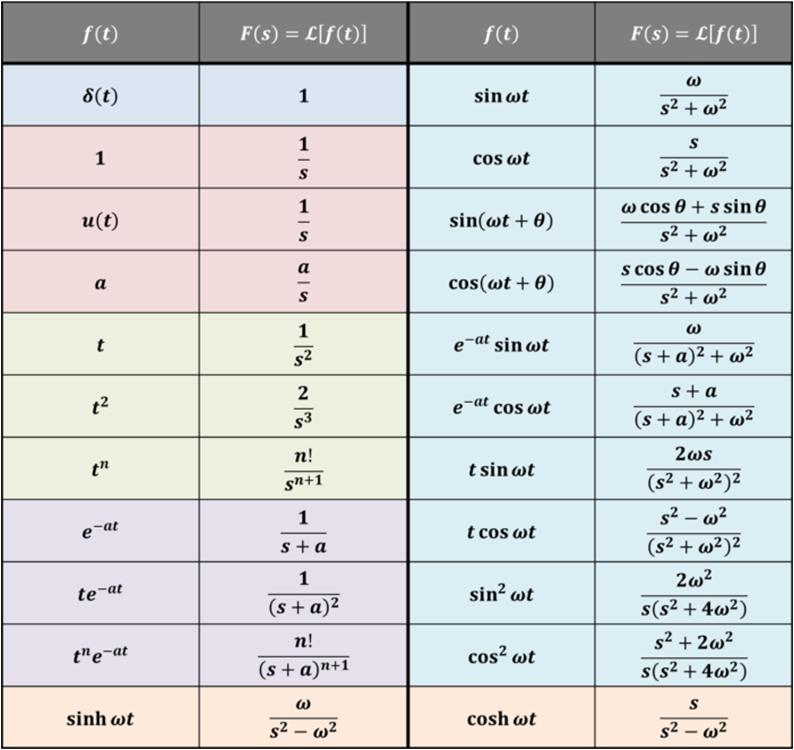
Fig. 1-2
※ https://detail-infomation.com/laplace-transform-table/
目次に戻る
具体例
例として右図のように RC 積分回路にステップ入力を与えたときの振る舞いについて、ラプラス変換を使って解いてみます。
まず、時間領域で微分方程式を立てます。
抵抗を流れる電流について、
容量を流れる電流について から
よって
以上から
が得られます。
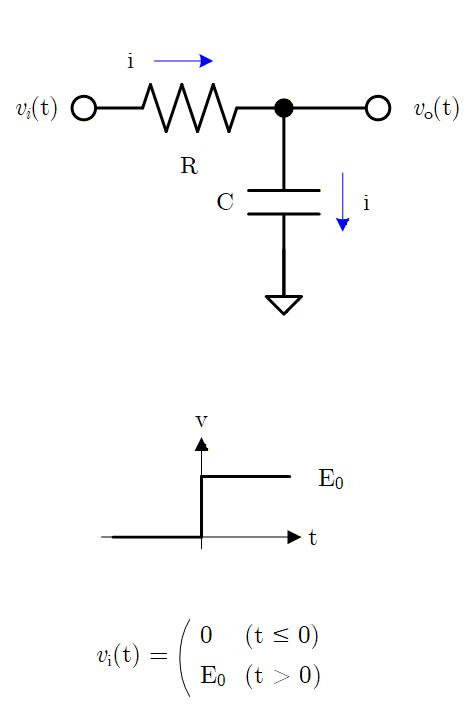
Fig. 1-3
(1) 式の各項をラプラス変換します。
はステップ関数だから、ラプラス変換すると になるので
とおいて整理すると
係数比較、あるいはヘビサイドの展開定理などを用いて部分分数に展開すると
ラプラス逆変換を行って時間領域の関数に戻すと
変換表を使ってラプラス逆変換を行うと
が得られます。
目次に戻る
伝達関数という考え方
先の例では、回路に対してある入力(関数) を与えたときの出力についての微分方程式を立てて、それをラプラス変換で解きましたが、
入力を変更するとその度に方程式を立てる必要があります。
なので、最初からラプラス変換された入力 に対する出力 の応答を伝達関数 として求め、各入力に対応する応答をみるときは の部分だけを変えてラプラス逆変換を行って を計算する方がラクです。 すなわち
→
→
という流れです。
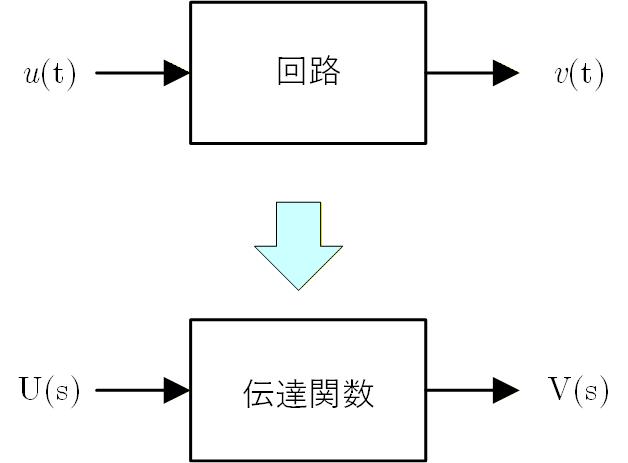
Fig. 1-5
目次に戻る
伝達関数の作り方
受動素子を使った回路については、それぞれの L, C, R のインピーダンスを直接ラプラス変換し、その Z(s) を回路トポロジ通りに組み上げることで、伝達関数が得られます。
各受動素子(インピーダンス) をラプラス変換するとどうなるかについては左図の通りになります。
抵抗はラプラス変換しても R のままですが、容量は電圧の微分が電流になるのでインピーダンスとしては 1/s が、インダクタンスは電流の微分が電圧になるのインピーダンスとしては s が、それぞれ付与されるかたちになります。
ちなみに、ラプラス変換されたインピーダンスの s を jω と置き換えると、電気回路でお馴染みの複素インピーダンスが得られます。
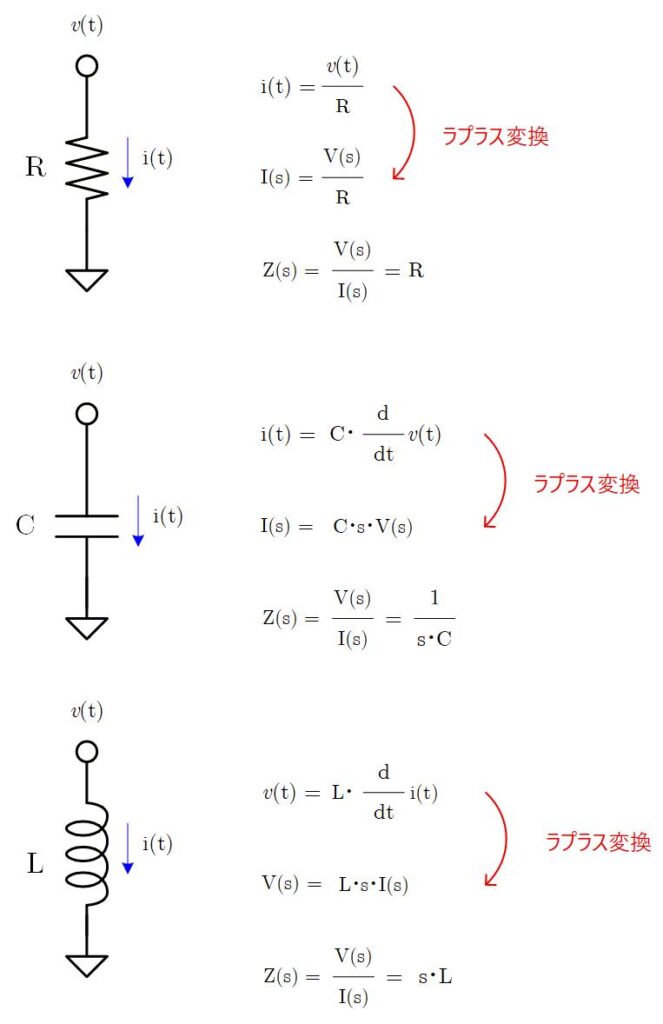
Fig. 1-6
これらのインピーダンスを組み合わせた回路の伝達関数は以下のように求めます。
先に使った RC積分回路を例にとって説明します。
出力 は入力 を と で分割した電圧になるので、以下の式で与えられます。
, を代入して を求めると、
は で得られるので、 を置き換えるだけで、その入力に対する出力 が求まり、前章でやったようにいちいち微分方程式を立てなくても簡単に計算ができます。
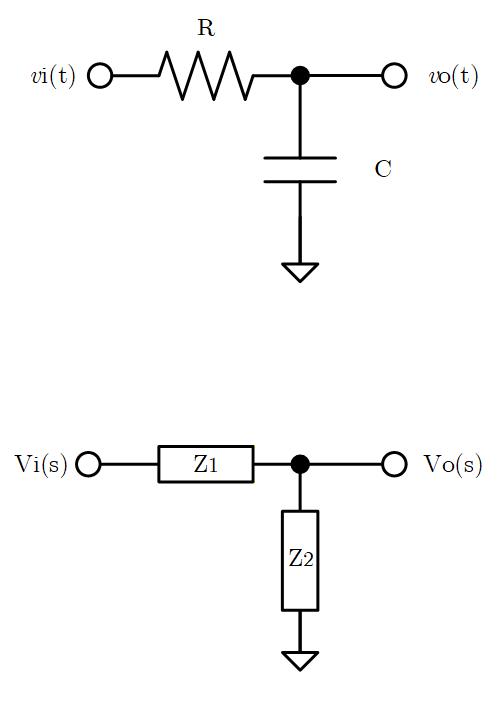
Fig. 1-8
ひとこと
トランジスタなどの能動素子は非線形素子なので直接ラプラス変換することはできませんが、前章で説明した小信号解析を行う場合は能動素子も線形素子とみなせるので、ラプラス変換可能になり、伝達関数として扱うことが可能となります。
目次に戻る
ラプラス変換を使った各種応答
この節では回路の伝達関数と、その回路の入出力応答について解説します。
一次遅れ要素の応答
RC 積分回路は一次遅れ要素とも呼ばれ、基本的な回路の一つです。 ここでは一次遅れ要素にさまざまな入力を与え、それらに対する応答をみていきます。
まずはじめに、一次遅れ要素の伝達関数を以下の式で表します。
これは前節で求めた RC積分回路の伝達関数の RC を、時定数 τ として置き換えたものになります。
以下、この伝達関数にさまざまな入力を与えたときの出力を調べて行きます。
目次に戻る
インパルス応答
インパルス応答とは、入力としてδ関数を与えたときの応答です。
実際に入力が δ関数として与えられることはありませんが、δ関数に近いインパルス波形として近似できるケースは多くあります。
出力のラプラス変換は
入力は δ関数だから なので
これをラプラス逆変換すると
が得られます。
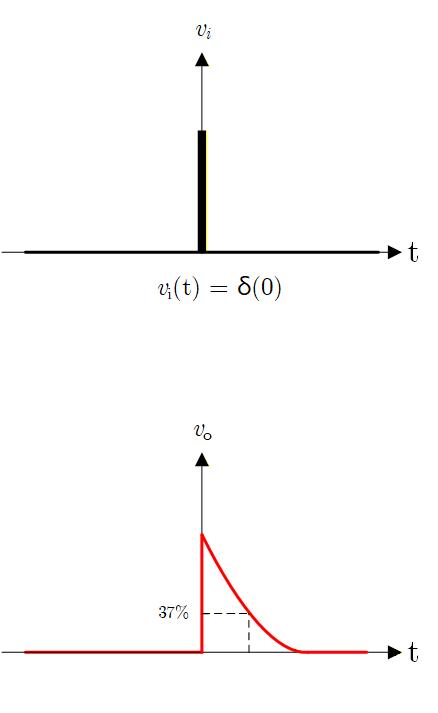
Fig. 2-1
目次に戻る
ステップ応答
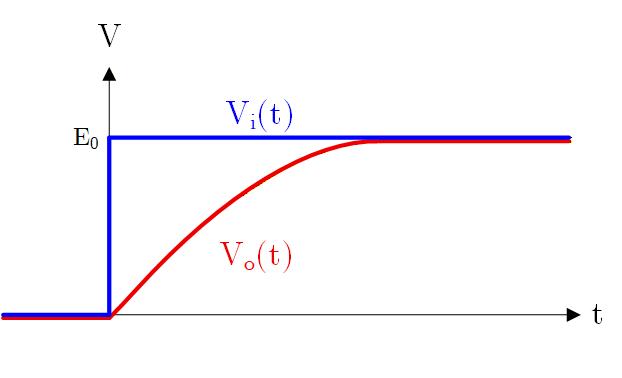
ステップ応答とは、入力としてステップ関数を与えたときの応答で、インディシャル応答とも呼ばれます。
実際に入力がある時刻でスパッと立ち上がることはありませんが、近似的にステップ状の波形として入力されるケースは多いです。
入力はステップ関数だから なので出力のラプラス変換は
ラプラス逆変換すると
得られます。
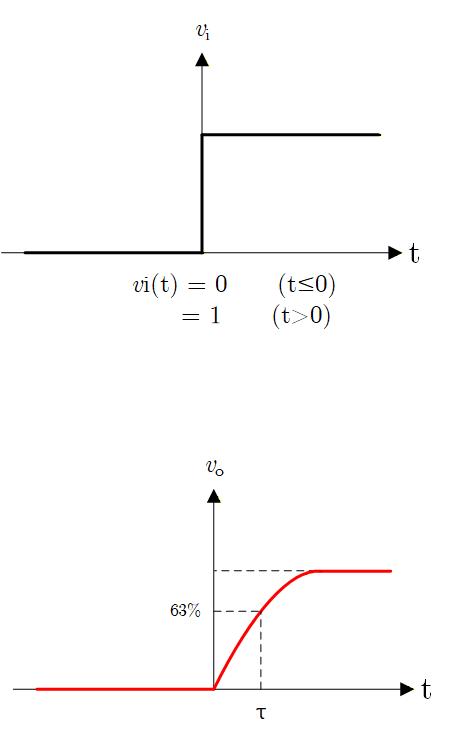
Fig. 2-2
目次に戻る
ランプ応答
ランプ応答とは、入力として時間とともに電圧がリニアに上昇するような関数を与えたときの応答です。
入力はランプ関数だから なので出力のラプラス変換は
部分分数展開すると
ラプラス逆変換すると
が得られます。
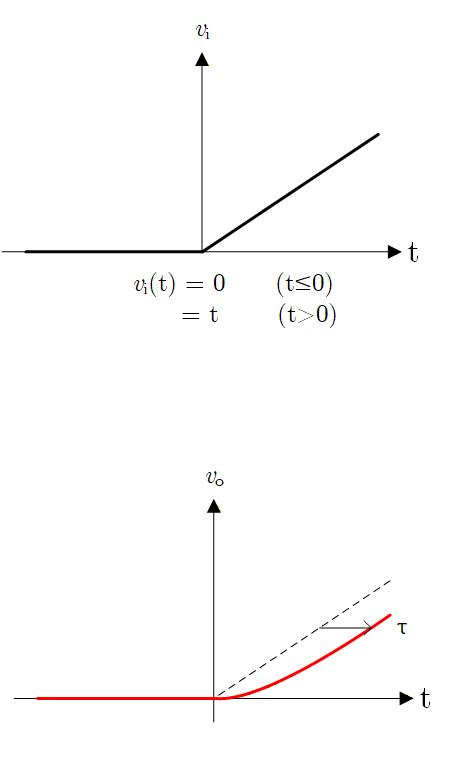
Fig. 2-3
こと
いずれの場合も、部分分数展開されることで最終的に出力には必ず伝達関数 による応答の項が含まれます。 残りは入力 による応答の項なので、計算しなくても想像がつきます。 ということで伝達関数 の部分のみをラプラス逆変換すれば、出力の振る舞いは予想できます。
目次に戻る
二次遅れ要素の応答
伝達関数の分母を特性方程式と呼び、特性方程式ががニ次式になる場合をニ次遅れ要素と言います。
2次遅れ要素の伝達関数の一般式は以下で表されます。
前節で述べたように伝達関数にのみ注目すれば振る舞いが分かるので、ここでは のインパルス応答のみを調べます。
特性方程式の解を -α,-β とおくと
部分分数に展開すると
これをラプラス逆変換すると
が得られます。
この振る舞いは、特性方程式の解、α, β が実数の場合と複素数の場合で大きく異なります。
解が実数の場合は式から明らかなように、時定数αと時定数βの2つの一次遅れ要素の応答の和になります。
解が虚数の場合は , として出力応答の式に代入すると
オイラーの公式から
となって、解が複素数の場合には時定数 σで減衰する項と、角周波数 ωで発振する振動項の積になります。
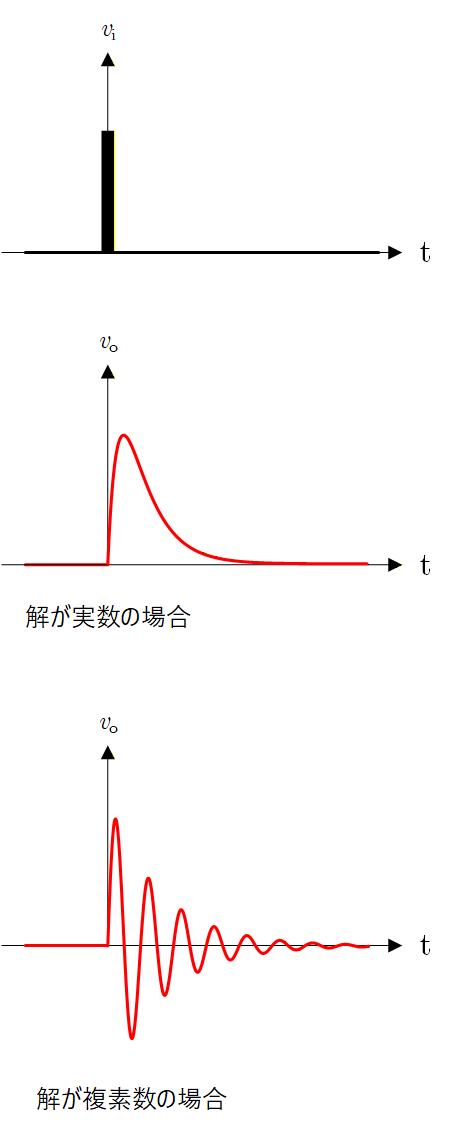
Fig. 2-4
目次に戻る
ニ次遅れ要素のダンピングファクター表現
二次遅れ要素の応答に関して、前節の特性方程式を ダンピングファクター (減衰比) を用いて表現すると、伝達関数は以下のように書けます。
この伝達関数はダンピングファクター (ζ) によってその振る舞いが変わります。 以下、場合分けをしてその振る舞いを調べていきます。
① ζ=0 の場合
ラプラス逆変換すると
結果は、角周波数 ω0 の正弦波となり、与えたインパルスにより引き起こされた振動が永続的に継続することになります。
② 0 <ζ<1 の場合
特性方程式の判別式は
で、ζ<1 なので D<0 となり、特性方程式は下記のように2虚根を持つことになります。
ここで , とおくと となるので
となります。
特性方程式が 2 虚根を持つ場合は先に述べたように応答は減衰項と振動項の積となります。
このとき、ζ が 0 に近いと ω >> σ となるので振動項が支配的で、ζ が 1に近いと ω << σ
となるので減衰項が支配的となります。
③ ζ= 1 の場合
D=0 なので特性方程式は重根を持ちます。
ラプラス逆変換すると
という応答が得られます。
④ ζ > 1 の場合
D > 0 なので特性方程式は 下記のように2実根を持つことになります。
応答特性は
が得られ、正の減衰項と負の減衰項の和になって、ζ が大きいほど収束が遅くなることがわかります。
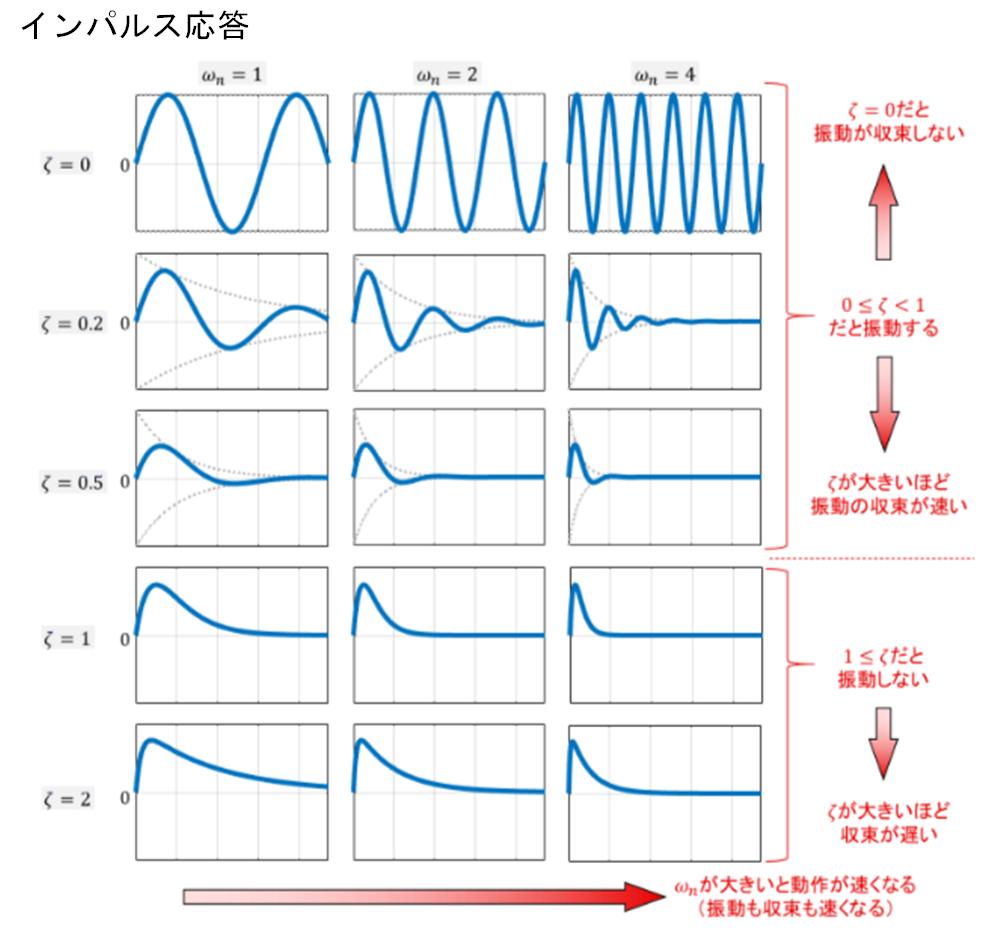
※ https://controlabo.com/second-order-system-impulse-step-response/
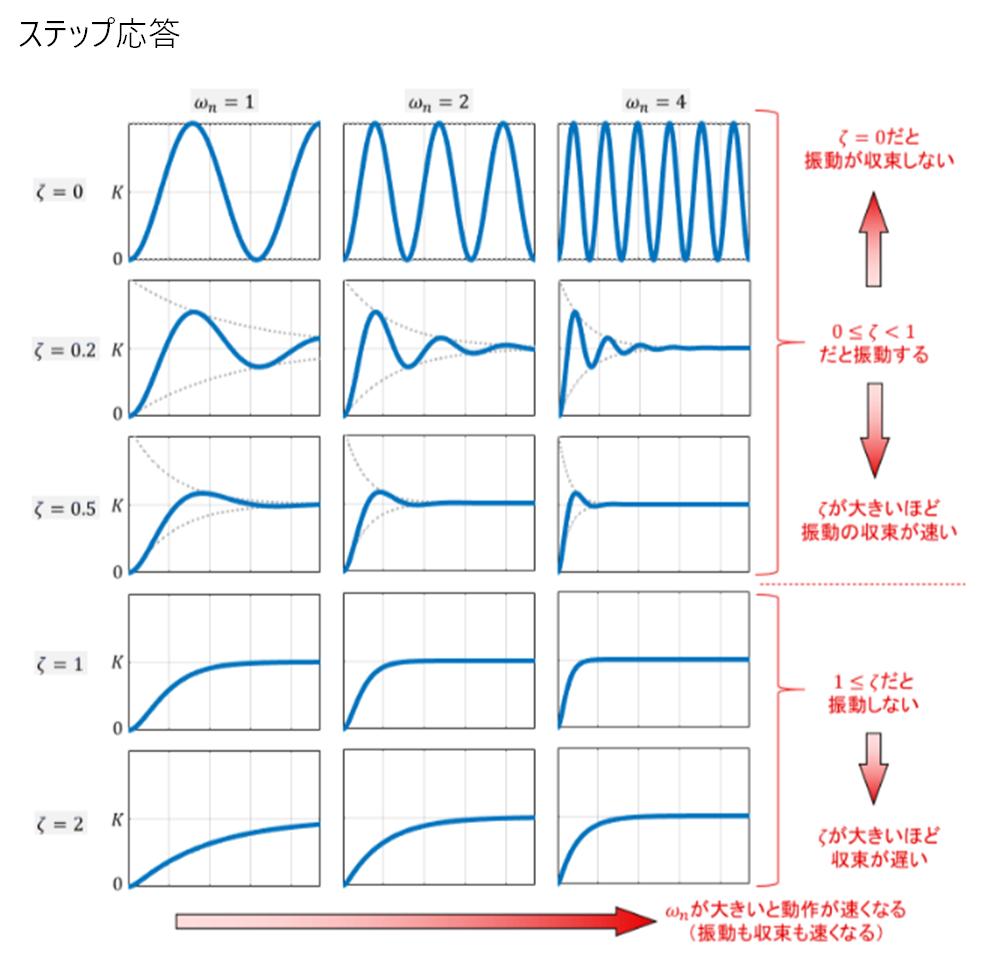
※ https://controlabo.com/second-order-system-impulse-step-response/
ダンピングファクター(減衰比、ζ)は、振動の減衰の度合いを示す数値で、ζ = 0 では振動は減衰せず、0 < ζ < 1 の範囲では ζ が0に近いほど振動が収まりにくく、ζ が 1に近いほど振動が早く収まり、 ζ ≥ 1 では振動は起きません。
ひとこと
一般に振動成分は嫌われるが、整定時間に着目すると全く振動しないより軽く振動する方が好ましく、ξ=0.5 〜 0.7 程度に設定するのが良いとされます。
目次に戻る
周波数応答
多くのアナログ回路では周波数応答が重要になりますが、これは伝達関数の ‘s‘ を ‘ jω ‘ と置き換えるだけで簡単に得ることができます。
ここでは一次遅れ要素を例にとって振る舞いを調べてみます。
まずは以下の一次の遅れ要素の伝達関数を考えます。
ここで、 とおくと
s を jωに置き換えると
となるので
が得られます。
ここから、周波数応答として注目すべき振幅と位相を求ると以下の結果が得られます。
振幅は、ω=0 で 0dB、 ω=ω0 で 1/√2 = -3dB、ω=∞ で 0 となり、位相は、ω=0 で 0°、ω=ω0 で -45°、ω=∞ で -90° となります。
ω0 をポール角周波数あるいはカットオフ角周波数などと呼びます。
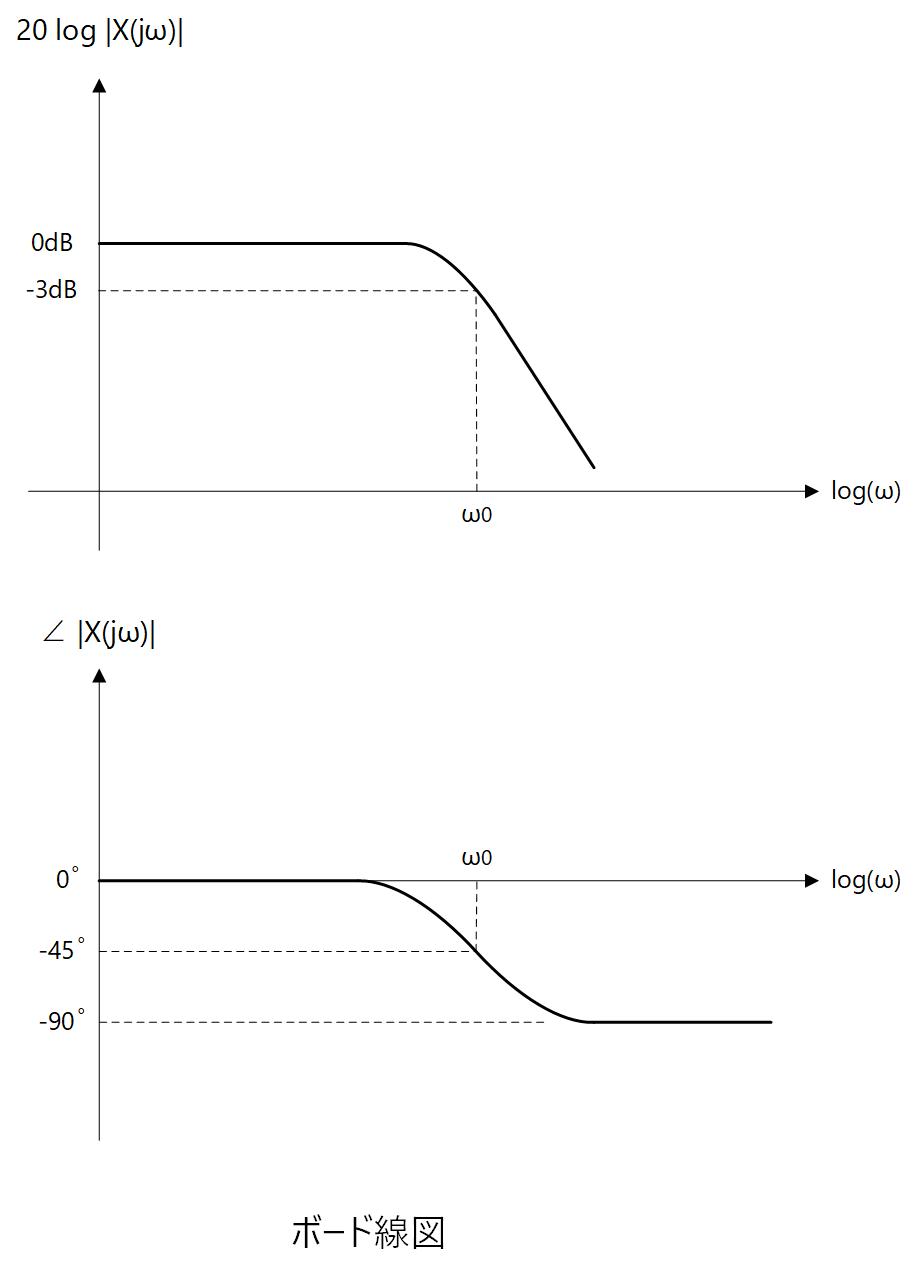
振幅と位相についてのグラフをひとまとめにしたものをボード線図と呼び、周波数応答・周波数特性を表現するもっとも一般的な方法です。
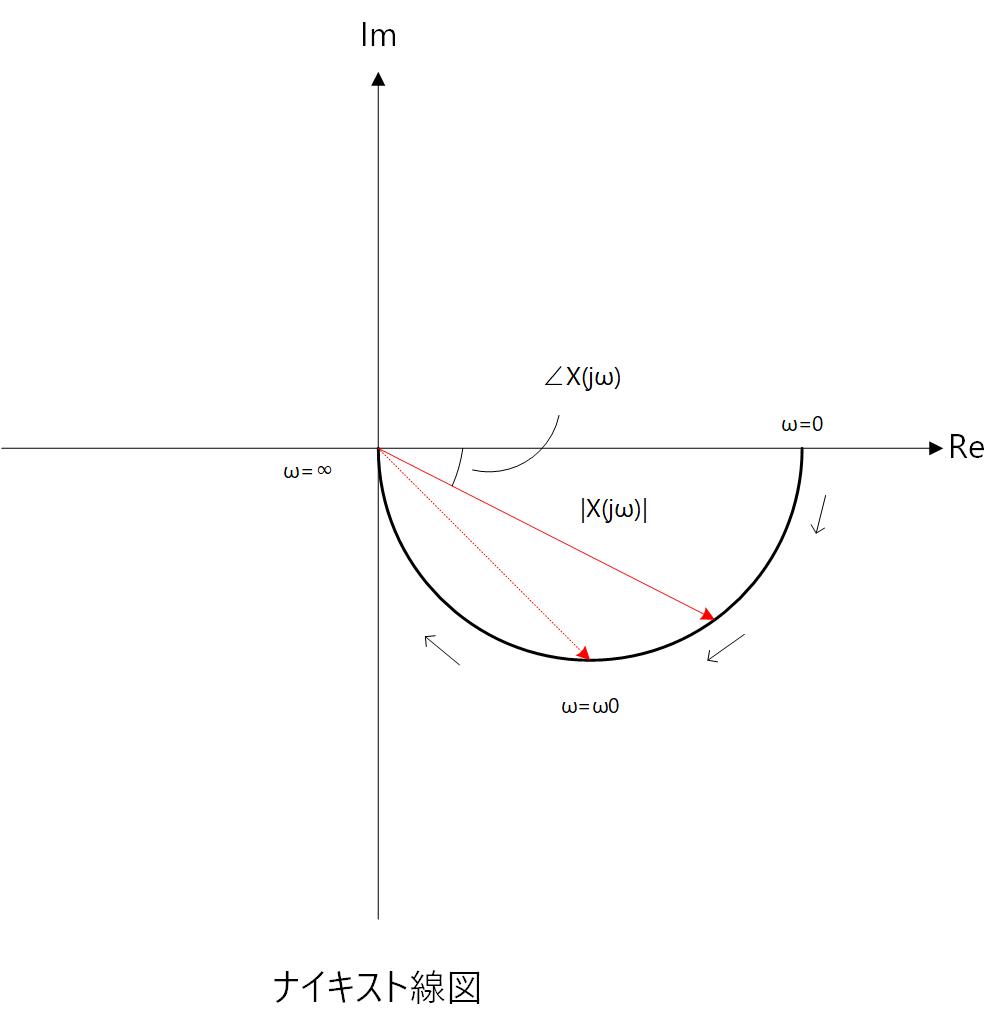
周波数特性を表現するもう一つの方法として、ナイキスト線図があります。
これは 横軸に の実数部、縦軸に の虚数部をとり、ω を媒介変数として ω=0 から ω=∞ までの軌跡を描いたものです。
ひとこと
s = jω とすることで何故周波数特性が得られるかについては Appendix を参照してください。
目次に戻る
まとめ
ラプラス変換を数学的に厳密に理解するのはかなり難しいですが、使うだけであればそれほどハードルは高くありません。
例えて言うなら、「車を運転するために車の構造まで理解する必要はない」 ということです。
もちろん構造まで知っていればそれに越したことはありませんが、車を運転して目的地に行くことが大事だと思います。
ということで、この講座では数学的な厳密性には目を瞑り、どのように使うかということに主眼をおいて説明してきました。
ラプラス変換はアナログ回路を学ぶ上では非常に有用なので、便利なツールとして割り切って使ってください。
目次に戻る
Appendix
回路の伝達関数が G(s) で表される場合、回路の周波数特性が G(jω) で得られる理由について解説します。
伝達関数 が、-s1, -s2,…., -sn の n 個の異なる極を持つと仮定すると、 以下のように書ける。
入力として u(t) = sin ωt の正弦波を与えると、出力は次式で求められます。
ここで、
とすると、 は以下のように部分分数展開できます。
ヘビサイト法を用いると、各係数は
よって
第1項は t →∞ でゼロとなる過渡項であるから、定常状態では第2項と第3項だけが残り
ここで、 , の関係から
以上から、
の入力に対して
となるため、入力の正弦波 に対して 出力 の正弦波は、振幅が 倍で、位相が だけ遅れた応答を示すことになり、伝達関数の周波数応答が で与えられることがわかります。
目次に戻る




















コメント