バルク半導体
真性半導体と不純物半導体
真性半導体
原子番号 14 の Si は最外殻の M殻に 4個の電子があり、単体では不安定ですが、結晶になるとお互いに M殻の電子を共有することで安定となります。
絶対零度では電子は原子核に束縛されて動かないため絶縁体として振る舞いますが、熱励起されると束縛を逃れる電子が現れ、残された場所には正孔が現れることで電気伝導に寄与するキャリアが発生します。 温度が高くなると励起されるキャリアの数は増加し、電気抵抗が下がっていきます。
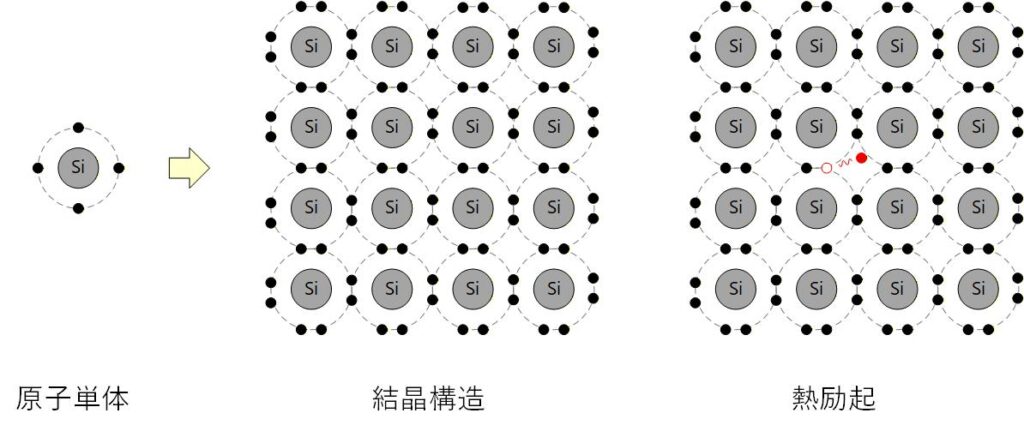
Fig. 1-1
不純物半導体
4価の Si に 5価の P などを不純物として添加すると、電子を与えるドナーとなり、電子がキャリアになります。
→ N型半導体 (Donner)
4価の Si に 3価の B などを不純物として添加すると、電子を受け取るアクセプタとなり、正孔がキャリアになります。
→ P型半導体 (Acceptor)
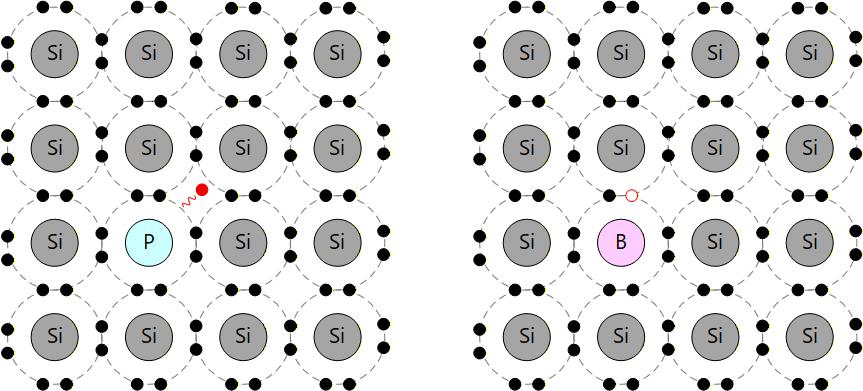
Fig. 1-2
暗黙の了解として、ここでは半導体はシリコンを意味します。
エネルギーバンド
電子と正孔のをバンド図で説明します。 価電子帯 (Valence Band) には電子が充満しており、熱や光などによって励起されると電子は伝導帯 (Conduction Band) に遷移してキャリアとなり、価電子帯に残された正孔もまたキャリアとなります。(Fig. 1-2a)
これを、Fig. 1-2a 右に示すように電子・正孔ともにフェルミレベルからの遷移と考えることができます。
バンドギャップの中心にフェルミレベルがある場合が真性半導体で、フェルミレベルから伝導帯までのエネルギー差とフェルミレベルから価電子帯までのエネルギー差が等しいため、電子のキャリア濃度() と正孔のキャリア濃度() は同じになります。 そのときの濃度を真性キャリア濃度 () と呼び、以下の関係が成り立ちます。
Fig. 1-2a の左図のようにバンドギャップの中心に対してフェルミレベルが伝導帯に寄っていれば 電子が増えて正孔が減り、N型となります。 逆に伝導帯の電子が Fig. 1-2b の右図のようにフェルミレベルが価電子帯に寄っていれば正孔が増えて電子が減り、 P型となります。
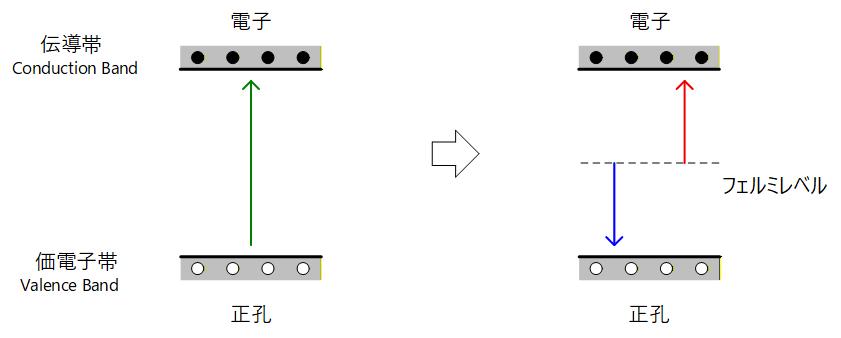
Fig. 1-2a
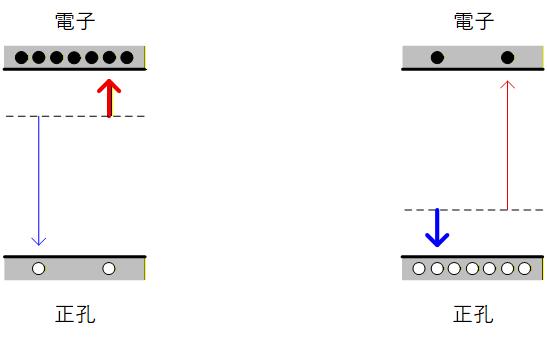
Fig. 1-2b
キャリア濃度
キャリア濃度を式で表すと以下のようになります。
ここで、 , はそれぞれ伝導帯・価電子帯の状態密度で、 , はそれぞれ伝導帯・価電子帯のエネルギー準位、 はフェルミレべルのエネルギー準位を意味します。
電子のキャリア濃度と正孔のキャリア濃度の積をとると、以下の関係が得られます。
Fig. 1-3a に真性半導体の場合の図を示します。
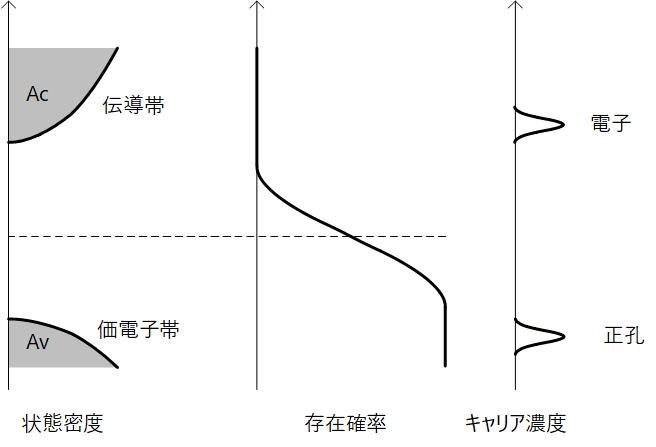
Fig. 1-3a
ここで、Eg はバンドギャップエネルギーで一定なので、
と書くと、以下のように表すことができます。
すなわち、電子のキャリア濃度と正孔のキャリア濃度の積をとると、それは真性キャリア濃度の自乗に等しくなります。
Fig. 1-3b に N型半導体、Fig. 1-3c に P型半導体の場合の図を示しますが、どんなときでも 電子のキャリア濃度(p)と正孔のキャリア濃度(n)の積は ni2 に等しくなります。
N型半導体の場合電子が多数キャリアで、電子のキャリア濃度はどれだけのドナー型不純物をドーピングしたかでほぼ決まります。
ドーピング濃度を とすると電子のキャリア濃度と正孔のキャリア濃度はそれぞれ、
と求めることができます。 ここで、具体的にキャリア濃度を求めてみると、真性半導体キャリア濃度は室温では [cm-3] 程度なので、アクセプタ不純物濃度を、 [cm-3] とすると
[cm-3]
[cm-3]
となり、少数キャリアである正孔は多数キャリアである電子の (=0.2ppb) しか存在しなことがわかります。 (ppb は 10億分の1 )
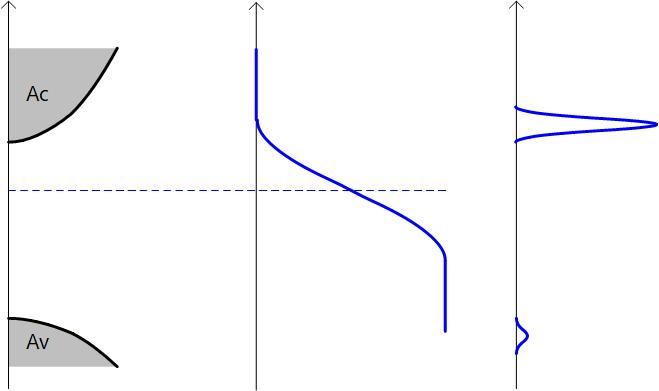
Fig. 1-3b
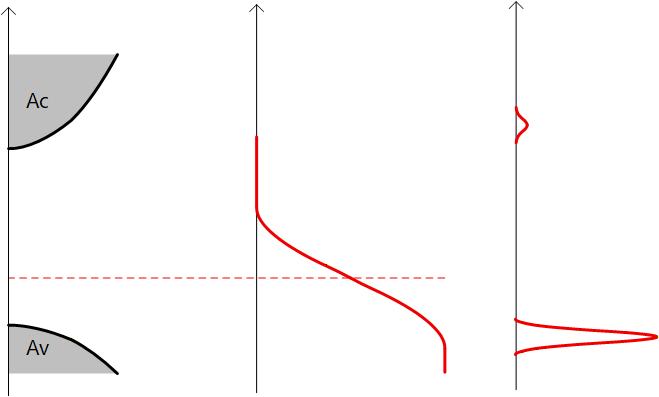
Fig. 1-3c
[cm-3] という不純物濃度は、普通使われるシリコン基板の濃度としてはかなり低いレベルです。
それでも、少数キャリアは多数キャリアの 0.2ppb しか存在しません。
なので、不純物半導体では通常は少数キャリアは電流には寄与しないことがわかります。
電流と連続の方程式
半導体で電流が流れるメカニズムは以下の3つに分けられます。
①ドリフト
キャリアに電界がかかると正のキャリアは電界の方向へ、負のキャリアは電界と逆方向に移動しますので、電流として観測されます。
ここで、 は電界強度で、 , はそれぞれ電子と正孔の移動度、 , はそれぞれ電子と正孔の濃度です。 (移動度は電界に対するキャリアの移動速度の比として定義されます)
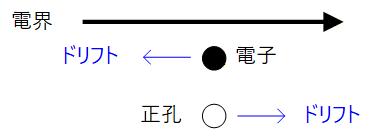
Fig. 1-4a
②拡散
キャリアに濃度の勾配があるとキャリアは濃度の高いほうから低い方へと流れます。 キャリアは熱運動により一定個所にはとどまらずに拡散するために、結果的にキャリアは濃度が高い方から濃度の低い方へと動くことになります。
ここで、 , はそれぞれ電子・正孔の拡散定数で、 , はそれぞれ電子・正孔の濃度勾配を表します。
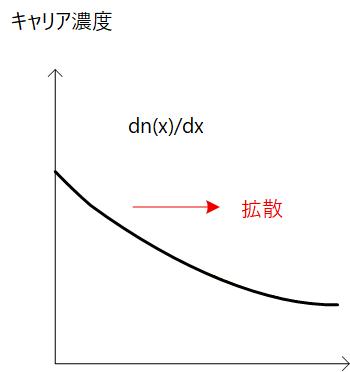
Fig. 1-4b
③発生と再結合
熱励起や光照射などがあると、電子と正孔が対として発生する現象があります。 また逆に電子と正孔ご再結合して消失する現象もあります。 このように発生と再結合か起こると、キャリア濃度自体が変化するために結果として電流に寄与することになります。
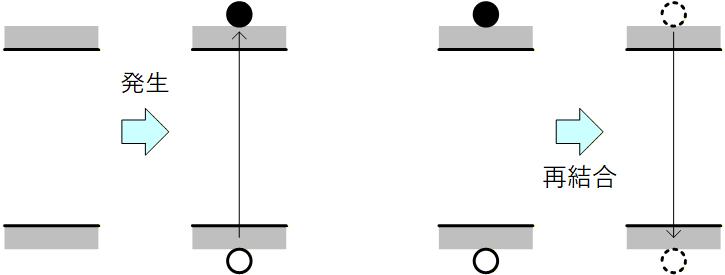
Fig. 1-4c
連続の方程式
ある閉じた領域を考えた場合、その領域に対してドリフト・もしくは拡散で流入するキャリアの数と、その領域からドリフト・もしくは拡散で流出するキャリアの数の差は、その領域で発生・再結合するキャリアの数に等しいという関係が常に成り立ちます。
これを連続の方程式と呼び、半導体での電流を考える上で非常に重要な式です。
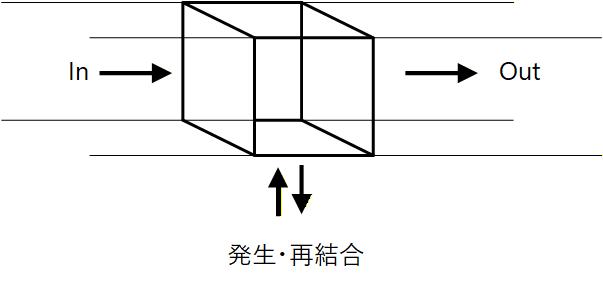
Fig. 1-4d
PN接合
平衡状態における PN接合
別個に存在する P型の半導体と N型の半導体を接合した場合を考えます。(Fig.2-1)
N型は電子が多数キャリアですが、P型では電子が少数キャリアになるため、拡散により電子は N型から P型に流れ込みます。同様に、正孔は P型から N型に流れ込みます。 N型では電子がなくなるため、残されたドナーイオンが正の空間電荷領域を形成し、逆に P型では残されたアクセプタイオンが負の空間電荷領域を形成するため、これらの空間電荷領域が電界を作ります。
この電界は拡散による電子・正孔の拡散を抑える方向に働くため、拡散電流とドリフト電流が釣り合ったところで平衡状態に落ち着くととになります。
空間電荷領域は空乏層や空乏領域とも呼ばれ、この領域にはキャリアは存在しません。
空乏層以外の P型領域ではアクセプタイオンと正孔が同数一様に存在し、N型ではドナーイオンと電子が同数一様に存在するため、それぞれ電気的中性領域となります。
これをバンド図を使って示すと Fig. 2-2 のようになります。
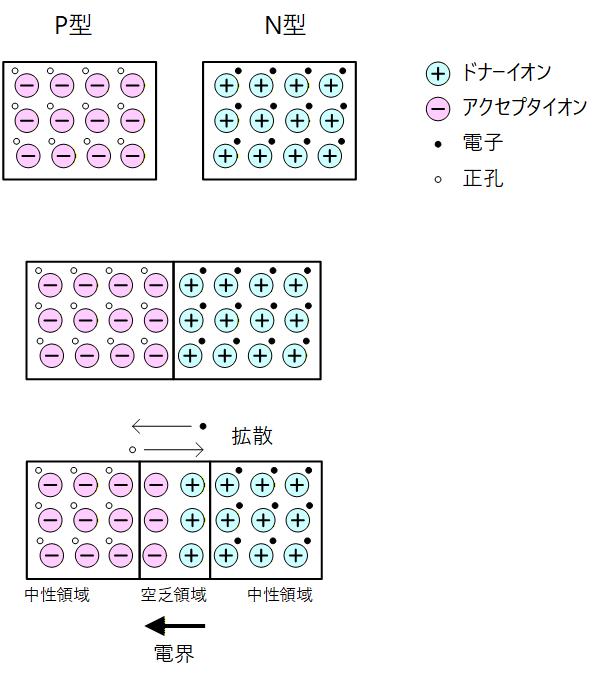
Fig. 2-1
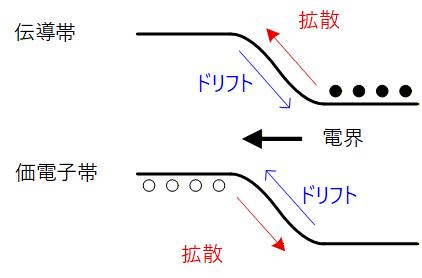
Fig. 2-2
平衡状態では P型半導体、および N型半導体のフェルミレベルが一致しますので、PN接合の境界では価電子帯と伝導帯のバンドに段差ができます。
これは作り付けの電位障壁(Built in Potential Barrier) と呼ばれ、その電位差によって形成される電界によって拡散が抑えられる仕組みです。
バンドが平坦な領域は中性電荷領域で、バルク半導体の状態と同じです。
バンドが曲がっている領域は空間電荷領域で、この領域ではフェルミレベルが伝導帯と価電子帯の両方から離れるため、電子・正孔ともに濃度が低い、空乏層を形成することになります。
順バイアス動作
PN接合は PNダイオードとも呼ばれ、整流作用があります。 ここではを順バイアスした場合について考えます。
Fig. 2-3 のように順バイアスがかかると電位障壁が下がり、N領域から P領域へ電子が流れ込み、逆にP領域からN領域に正孔が流れ込み、結果として P領域からN領域へと電流が流れることになります。
このように P領域では本来少数キャリアである電子が N領域から注入され、逆にN領域では本来少数キャリアである正孔が P領域から注入されることになります。 これを少数キャリアの注入と呼びます。
もう少し物理的に説明します。
バイアスがかからない状態は平衡状態なので、P型に対してもN型に対してもフェルミレベルは等しくなりますが、バイアスがかかるとフェルミレベルは価電子帯に対する擬フェルミレベルと伝導帯に対する擬フェルミレベルに分離します。
P領域では価電子帯と電子に対する擬フェルミレバルの距離が近づくため、電子のキャリア濃度がゼロバイアス時に対して増えることになり、N領域では伝導帯と正孔に対する擬フェルミレバルの距離が近づくため、正孔のキャリア濃度がゼロバイアス時に対して増えることになり、
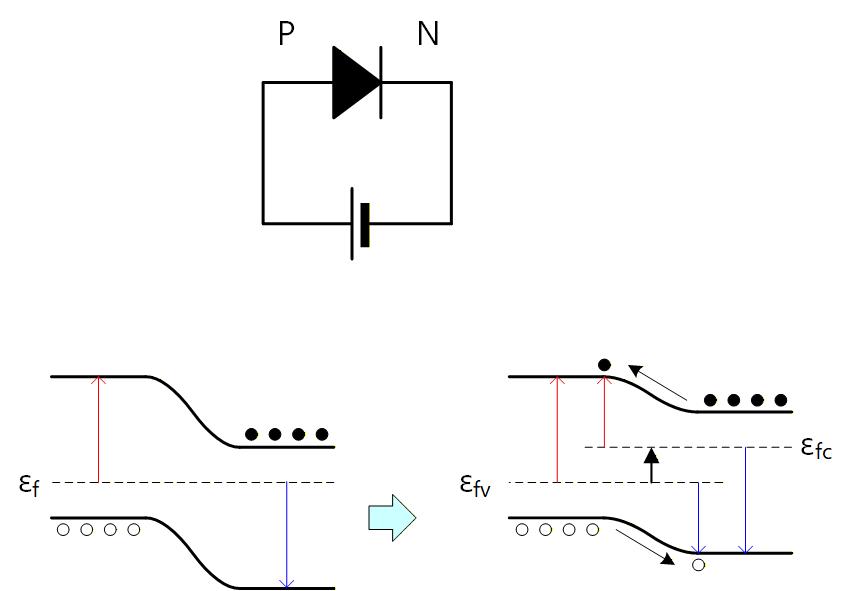
Fig. 2-3
逆バイアス動作
PN接合を逆バイアスした場合を考えます。
Fig. 2-4 のように逆バイアスがかかると電位障壁が高くなり、P領域における少数キャリアである電子がN領域に、逆にN領域における少数キャリアである正孔が P領域に、それぞれ無理やり引き抜かれることで電流が流れます。
しかし、それぞれ少数キャリア濃度はもともと低いため電流は極めて小さく、逆方向電流はほとんどゼロです。
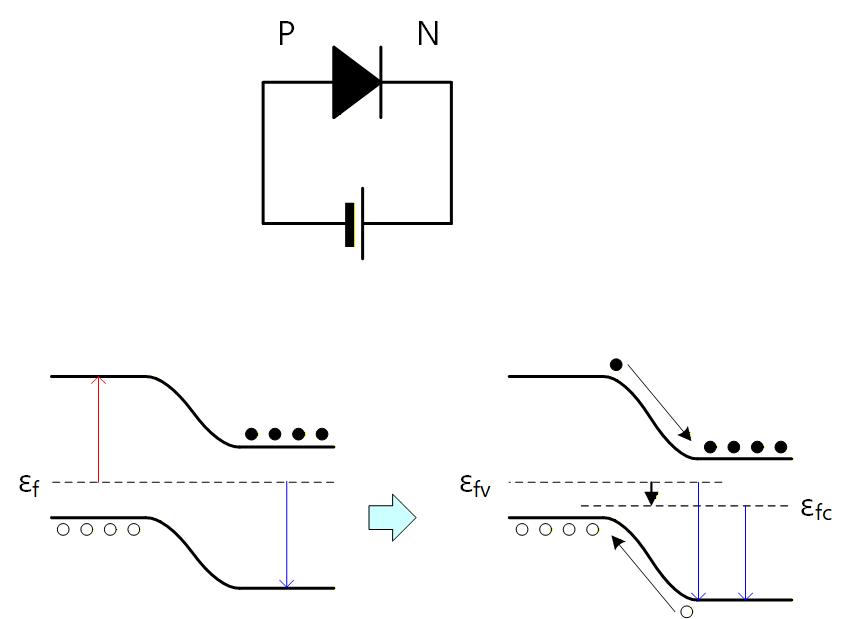
Fig. 2-4
電流の式
以上みてきたように、PN接合に順バイアスを印加すると電流が流れ、逆バイアスを印加した場合には電流が流れないという、いわゆる整流作用があります。 このような PN ダイオードにおける電流の式は以下のように書けます。
ここで Is は逆方向飽和電流と呼ばれ、例えば などの極めて小さい値を取りますのて、逆方向電流は非常に小さいことがわかります。
一方で となる順バイアスがかかると電流の式は以下のように書け、実際にダイオードを使う場合には妥当な近似になります。
式から明らかなように、ある程度の順バイアスがかかると電流は指数関数的に増大するため、順方向バイアス電圧は飽和するとみなせます。 これを順方向飽和電圧と呼ぶこともあり、その値は 0.6〜0.7V 程度となります。
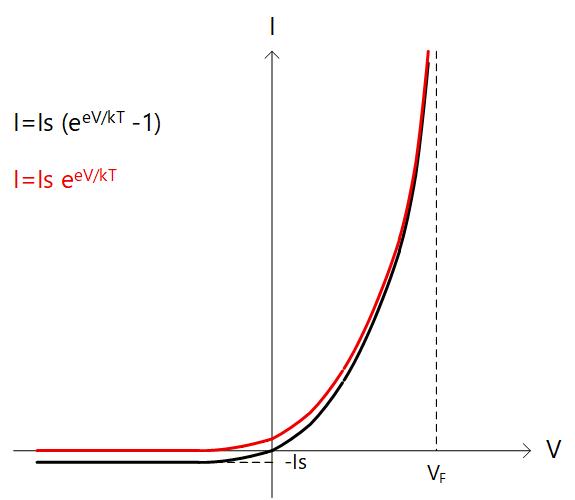
Fig. 2-6
接合容量
空乏層ではキャリアが存在しないため、誘電体として振る舞います。一方、その両端は中性領域なので導電体として振る舞います。
なので、空乏層は並行平板コンデンサとみなすことができ、空乏層の幅を d とすると、
となります。 ここで、 は真空の誘電率で、 はシリコンの比誘電率 (≒11.7) になります。
実際には PN接合に印加するバイアス電圧によって空乏層の幅は変化するため、接合容量はバリキャップとして振る舞い、近似的に以下の式で表されます。
ここで、 は逆バイアス電圧で、 は , で決まる定数です。 逆バイアスを深くすると空乏層は広がり、容量は小さくなります。
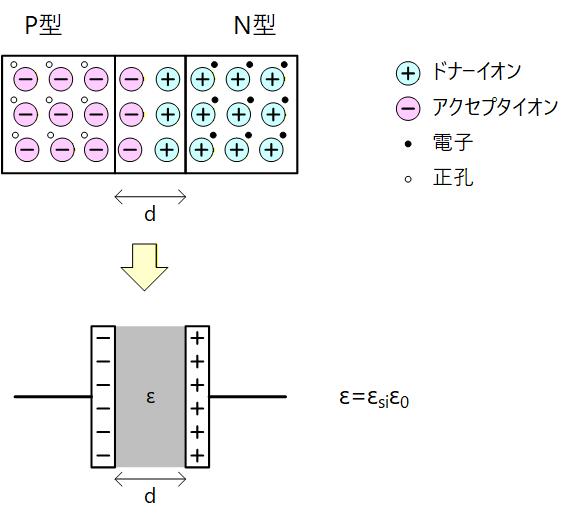
Fig. 2-7
MOS トランジスタ
MOS 構造とフラットバンド電圧
MOS 構造とは、Fig. 3-1a のような Metal-Oxide-Semiconductor の3層からなり、MOSトランジスタの骨格をなす重要な構造です。
Metal は金属、Semiconductor は半導体、Oxide 酸化膜を意味します。
一般的な半導体プロセスでは、Metal はポリシリコンを用い、Semiconductor は結晶シリコンで、Oxide はその結晶シリコンを熱酸化することで形成します。
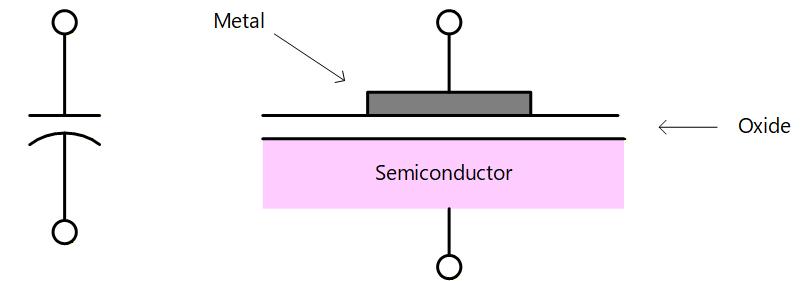
Fig. 3-1a
Fig. 3-1b は、Metal, Oxide, Semiconductor が離れて存在するときのバンド図です。
仕事関数は、フェルミレベルにある電子を真空の準位に満ち上げるためのエネルギーで、Metal と Semiconductor では異なる値を取ります。
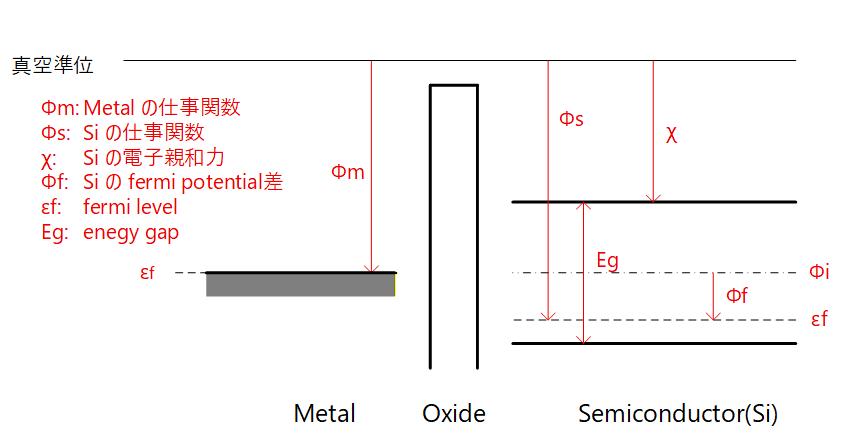
Fig. 3-1b
Fig. 3-1c はそれらを同電位で接触させたときのバンド図になります。
平衡状態なので、Metal に対するフェルミレベルと Semiconductor に対するフェルミレベルが等しくなるため、仕事関数差の違いによりバンドが曲がります。
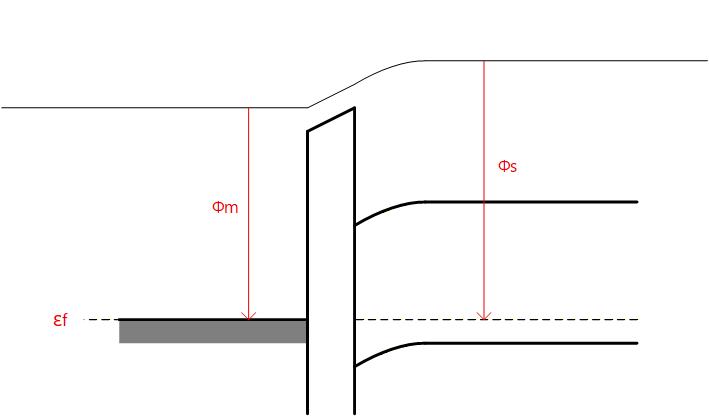
Fig. 3-1c
Fig. 3-1d は、Metal と Semiconductor の間に Vfb という電圧をかけて、バンドがフラットになったときのバンド図で、Vfb をフラットバンド電圧と呼びます。
MOS 構造を考える上では、このフラットバンド状態が基準となります。
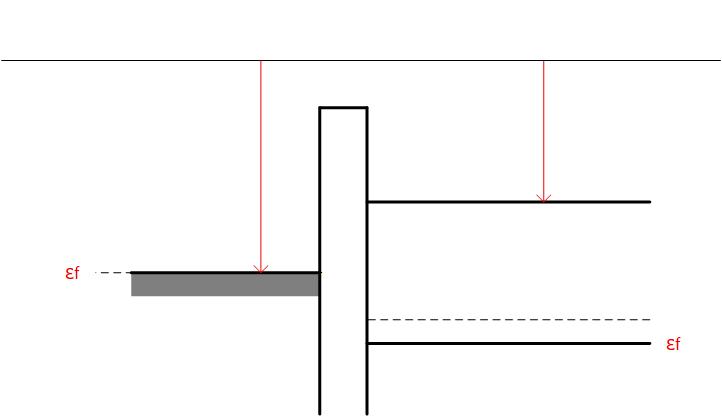
Fig. 3-1d
古くは MIS (Metal-Insulator-Semiconductor) とも呼ばれました。
Insulator は絶縁体で、絶縁膜を熱酸化で作ることで界面準位の問題を解決して今に至るため、最近では MOS 構造と称することが一般的です。
厳密にはフラットバンド電圧は仕事関数差だけで決まるわけではありませんが、そういう理解で特に問題ありません。
MOS 構造における蓄積・空乏化・反転
いま Semiconductor として、P型Si の場合で考えます。
P型Si では多数キャリアは正孔で、ここでは話を簡単にするために Fig. 3-2a 左の図のように Metal と Si を短絡した時、すなわち両者のフェルミレベルが等しい時にフラットバンド条件を満たしているものと仮定します。 この状態では、バンドの曲がりはないため、Si 基板の表面でも奥でも、その正孔の濃度は同じです。
ここで、Fig. 3-2a 右の図のように Metal に負電圧を印加すると、バンドが上方向に曲がります。
Si の表面 (Si-SiO2 界面) に注目すると、価電子帯がフェルミレベルに近づくため多数キャリアである正孔が増加します。
この状態を “蓄積 = Acumulation” と呼び、MOS構造は SiO2 膜を誘電体層とする並行平板コンデンサとして働き、SiO2 の膜厚を Tox とすると単位面積あたりの容量は、
で与えられます。 (εox は SiO2 の比誘電率で、約 3.9)
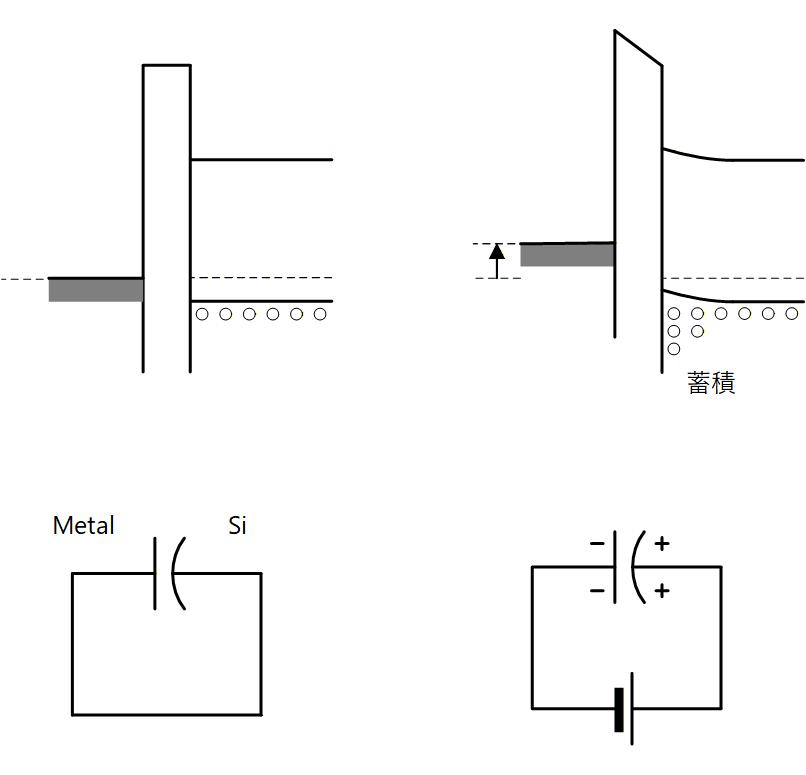
Fig. 3-2a
次に Fig. 3-2b 左のように Metal に正電圧を印加した場合を考えます。
正電圧をかけたときには、左図のようにバンドが下方向に曲がります。
Si の表面 (Si-SiO2 界面) に注目すると、価電子帯がフェルミレベルから遠ざかるため多数キャリアである正孔が排斥され、濃度が極端に減少します。
この状態を “空乏化 = Depletion” と呼び、MOS構造は酸化膜容量と空乏層容量の直列接続容量のように振る舞います。
Oxide の膜厚を Tox し、空乏層の深さを ldep とすると単位面積あたりの容量は、
で与えられます。 (εsi は Si の比誘電率で約 11.9)
酸化膜容量に空乏層容量が直列接続されるため全体としての容量は酸化膜容量よりも小さくなります。
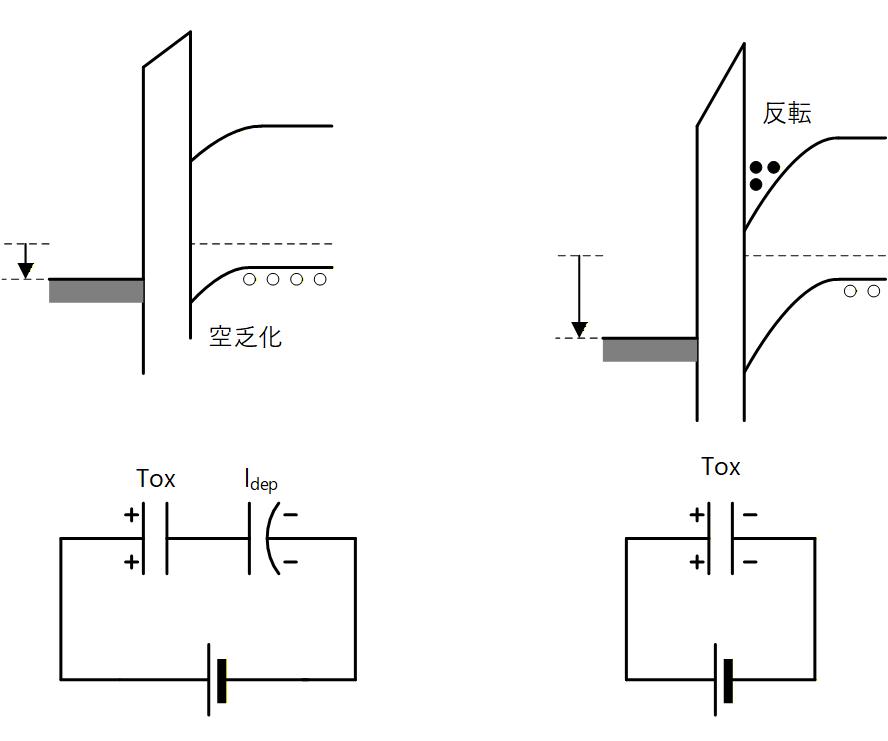
Fig. 3-2b
続いて Metal にさらに高い正電圧を印加した場合を考えます。
この場合は、 Fig. 3-2b 右のようにバンドが下方向に大きく曲がります。
Si の表面(Si-SiO2 界面) に注目すると、今度は伝導帯がフェルミレベルに近づくことになり、少数キャリアの電子が誘起され、P型半導体でありながら電子が発生します。この状態を “反転 = Inversion” と呼びl、MOS構造は再び酸化膜容量のみが見えてくる容量として働くようになります。
どこからを反転と呼ぶかは明確には決まっていませんが、P型であれば反転電子の濃度が、本来多数キャリアである正孔の濃度と等しくなったところとすることが一般的です。
以上の振る舞いをグラフにすると 右のようになります。
負電圧印加の場合は Si 表面には多数キャリアの正孔が蓄積されるため酸化膜容量が見えます。正電圧を印加して空乏層が発生すると、多数キャリアの正孔が表面から排除されることで、酸化膜容量に空乏層容量が直列接続された容量ご見えるので、容量としては酸化膜容量から減少します。
さらに高い正の電圧を印加すると、Si 表面に反転電子が誘起されることで、容量としては再び酸化膜容量だけがみえてくるようになります。
ひとつ注意事項としては、この MOS 構造が単体として存在する場合には、”反転” が起きるまでには十分な時間が必要になることが挙げられます。
電圧印加でバンドが曲がって平衡状態に達すれば、フェルミレベルと伝導帯の間隔に相当する電子が現れますが、過渡状態では直ぐには反転電子は現れません。 熱励起により電子・正孔対が「発生」することで電子が Si表面に出現するため、ある程度時間がかかることになります。
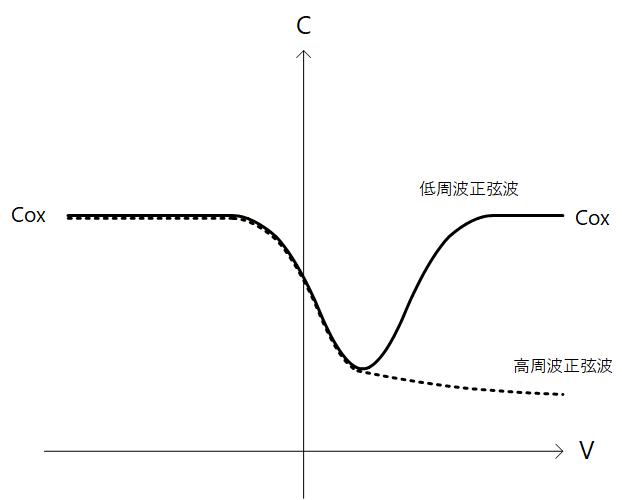
Fig. 3-3 のグラフは実線が低周波の正弦波を与えたときの容量で、破線が高周波の正弦波を与えたときの容量になります。
低周波の場合は反転電子が集まる十分な時間があるため反転層ができますが、高周波の場合には反転電子は集まる時間が確保できないため反転層はできないため、容量としては酸化膜容量と空乏層容量の直列接続容量が見えることになります。
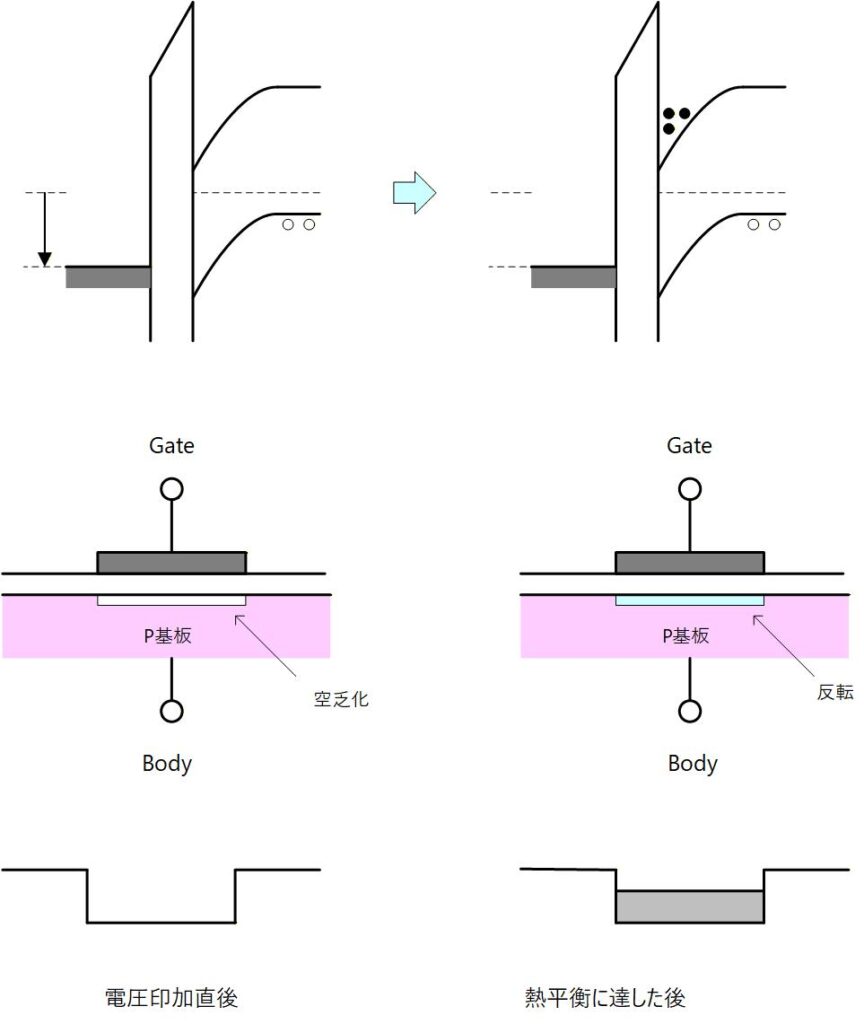
Fig. 3-4
ここでは熱励起によるキャリアの発生で説明しましたが、光励起によっても熱励起と同様に反転電子が Si 表面に蓄積されます。 この現象がイメージセンサーに使われます。
MOS トランジスタの構造とポテンシャル記述
前節で、MOS 構造単体では反転電子が Si 表面(Si-SiO2 界面)に蓄積されるには時間がかかると説明しましたが、Fig. 3-5 に示すようにMOS 構造に隣接して電子の供給源となる N型領域を設けると、そこからMOS構造の Si 表面に反転電子が供給されるため、高周波の電位変化に対する応答性が劇的に向上します。この構成を MOS 容量と呼びます。
以降、Metal電極を Gate、P型 Si を Body、N領域を Source 、Si-SiO2 界面の反転電子が存在しうる領域を Channel と言い換えると、MOS 容量で起こる現象は以下のように説明できます。
「Gateにあるしきい値以上の高い正電圧を印加すると、Gate下に Channel が形成されます。 MOS構造に隣接して Source を配置すると、 Source から Channel に電子が供給され、Channel には電子が満たされます。」
これをバンド図で示すと Fig. 3-6 のように MOS 構造の Si-SiO2 界面に、隣接する N領域から多数決キャリアの電子が供給されることになります。
この状態で Gate 電圧が微小変動すると、 Channel 電位 (=Channel ポテンシャル) もそれに連動して変化し、Channel に蓄積される電子の数も変化するので、容量として働くことになります。
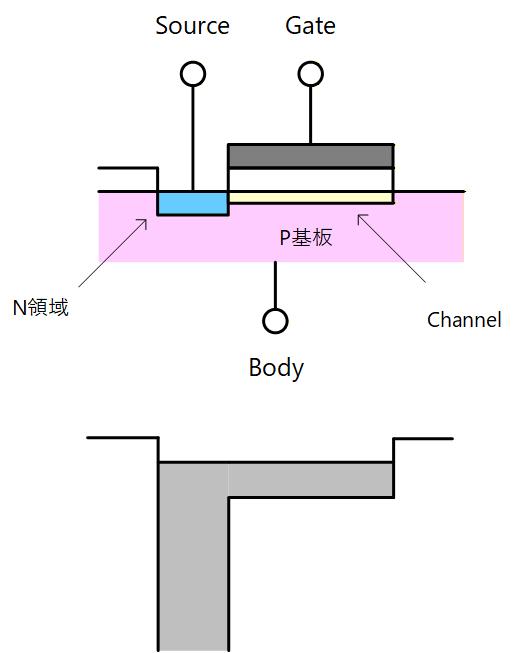
Fig. 3-5
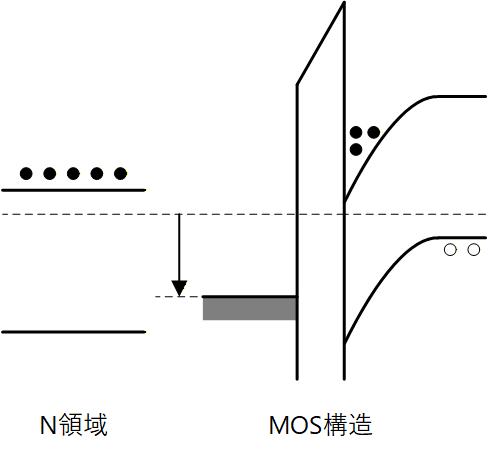
Fig. 3-6
次に、Fig. 3-7 に示すように Source の反対側に電子を排出する N領域を追加してみます。
このN領域を Drain と呼び、Drainには Source よりも高い電圧、すなわち低いポテンシャルを与えます。
すると、Source から注入された電子は Channel を通って Drain へと排出されることになります。
これが MOSトランジスタです。
ここで、Gate 電圧が低いと Channel が形成されないため電流は流れません。
Gate電圧を高くすると Channel が形成されて Source から電子が注入されて Drain に排出されることで電流が流れます。
Gate電圧をさらに高くすると Channel 下の電子数が増えて電流は増加します。
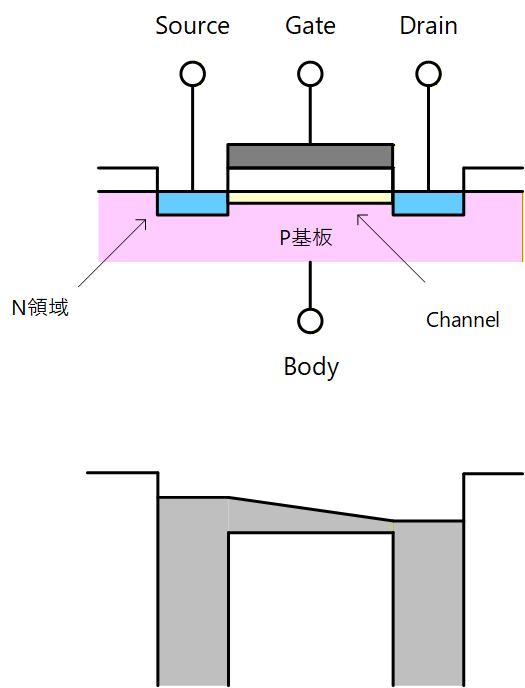
Fig. 3-7
ポテンシャル図による動作把握
Fig. 3-8 のように、MOSトランジスタの Source とBody を接地し、Drain に定電圧を与えた状態で Gate 電位を 0V から高い電圧に Sweep していったときの状態の変化を ポテンシャル図で考えます。
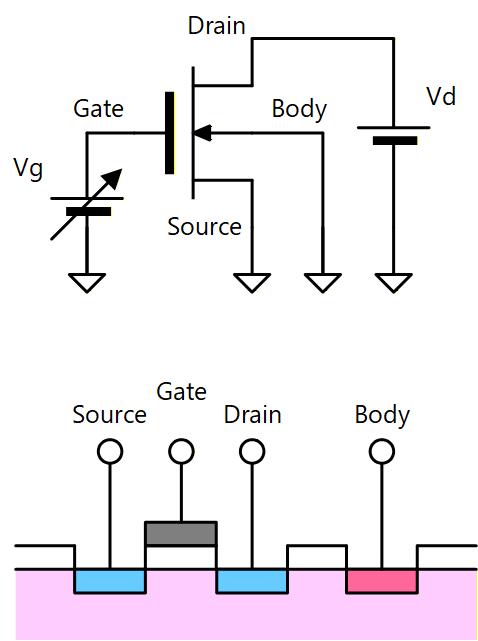
Fig. 3-8
遮断
Vg=0V のときには Channel のポテンシャルは下がらず、電子は存在しないために電流は流れません。 この状態を “遮断状態” である、または “遮断領域” にいると言います。
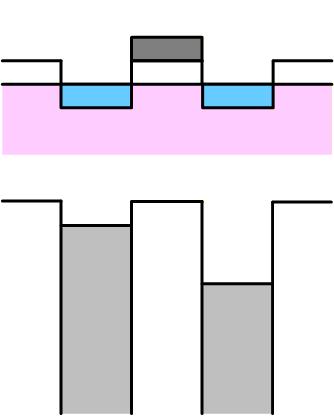
Fig. 3-9a
しきい値
Gate電圧を高くしていくと Channel ポテンシャルが下がり、Source のポテンシャルと等しくなります。 このときの Gate 電圧を “しきい値電圧” と呼び、 Vth あるいは Vt などと表します。
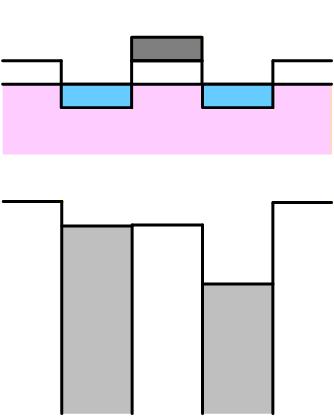
Fig. 3-9b
5極管
Gate電圧をしきい値電圧より高くすると、 Channel ポテンシャルは Source 電位より下がり、Source から Channel に電子が注入されます。 注入された電子は Source-Drain 間の電界によりドリフトし、Drain に達することで、Source-Drain 間に電流が流れます。
この場合の電流は ChannelポテンシャルとSource の電位のみで決まり、そのポテンシャルの差が大きくなると電流は増えます。
Channelポテンシャルは Gate 電圧で決まるので、Gate 電位とSource電位のみで決まると言って構いません。 この時、Drain 電圧が変化しても電流は変わりません。
この状態を “5極管状態” である、または “5極管領域” にいると言います。
(MOSトランジスタに限定すると “飽和領域” と呼びます)
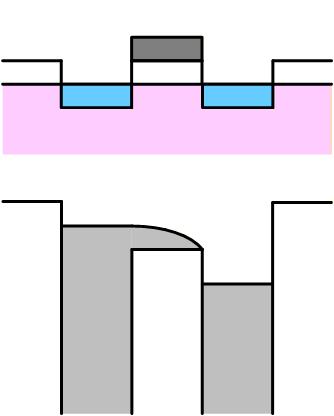
Fig. 3-9c
3極管
Gate電圧をさらに高くして、Channelポテンシャルが Drain電位より下がるようになります。 この状態では 5極管領域とは異なり、流れる電流は Drain 電圧に対しても感応度を持ちます。 この状態では Gate電圧が高くなった場合には Channel 下の電子濃度が増加するために、また Drain電圧が高くた場合には Source-Drain 間の電界が強くなるため、どちらの場合も電流は増加します。
この状態を “3極管状態” である、または “3極管領域” にいると言います。
(MOSトランジスタに限定すると “線形領域” と呼びます)
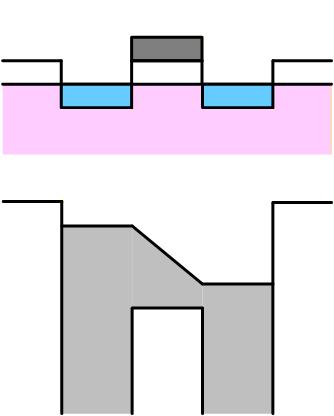
Fig. 3-9d
以上の関係をグラフにすると以下のようになります。 これは Gate-Source間の電圧に対する Source-Drain 間電流の関係を表すので、Vgs-Ids 特性、あるいは単に Vg-Id 特性とも呼ばれます。
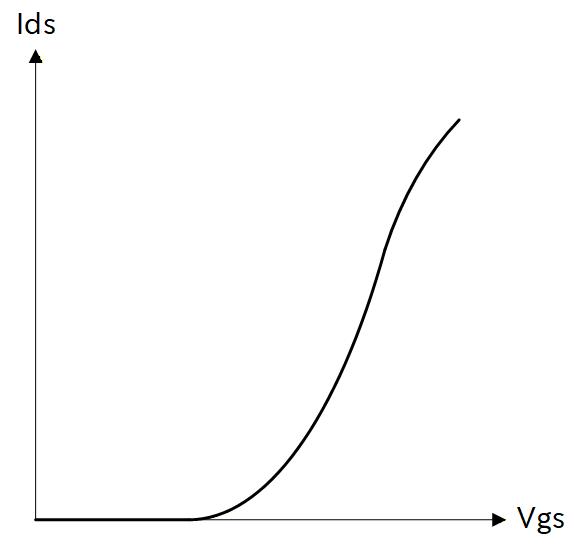
Fig. 3-10
続いて右図のように、MOSトランジスタの Source とBodyを接地し、Gate にしきい値電圧 Vth より高い定電圧を与えた状態で Drain 電圧を 0V から高い電圧に Sweep していったときの状態の変化を ポテンシャル図で考えます。
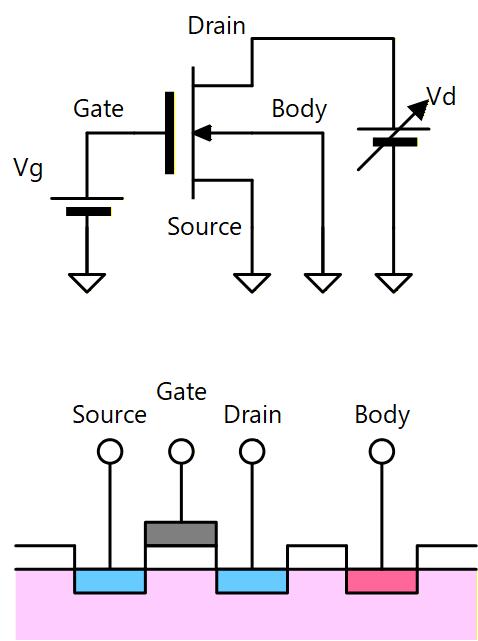
Fig. 3-11
導通
Vd=0V のときには Source-Drain 間の電位差はないため、Channel に反転電子が存在しても電流は流れません。 ただし、これは “遮断状態” ではありません。 あくまでも Source と Drain は導通状態で、3極管状態の極端な場合として理解してください。
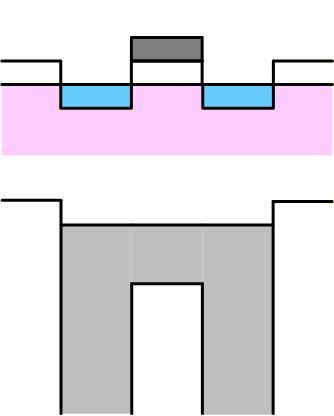
Fig. 3-12a
3極管
Drain電圧が高くなると、Channel には電子が誘起されてますので Source-Drain 間の電位差に応じた電流が流れます。 また図からわかるように 3極管状態ですので、電流は Channel ポテンシャル、すなわち Gate 電圧にも依存します。
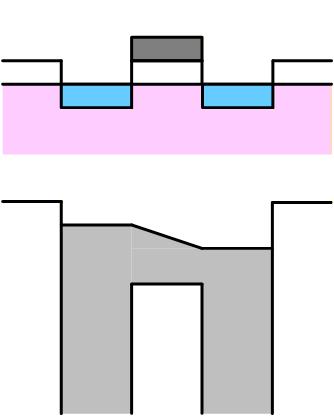
Fig. 3-12b
5極管
Drain電圧をさらに高くして、Channelポテンシャルが Drain電位より下がると 5極管領域となり、電流は Drain電圧によらずに一定(飽和)となります。
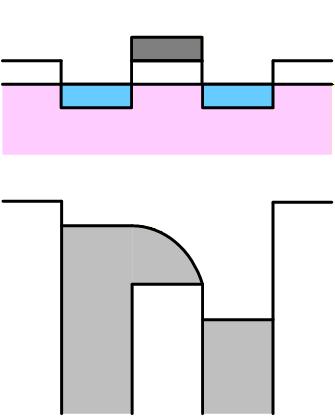
Fig. 3-12c
以上の関係をグラフにすると Fig. 3-13 のようになります。 これは Drain-Source間の電圧に対する Drain-Source 間電流の関係を表すので、Vds-Ids 特性、あるいは単に Vd-Id 特性とも呼ばれます。
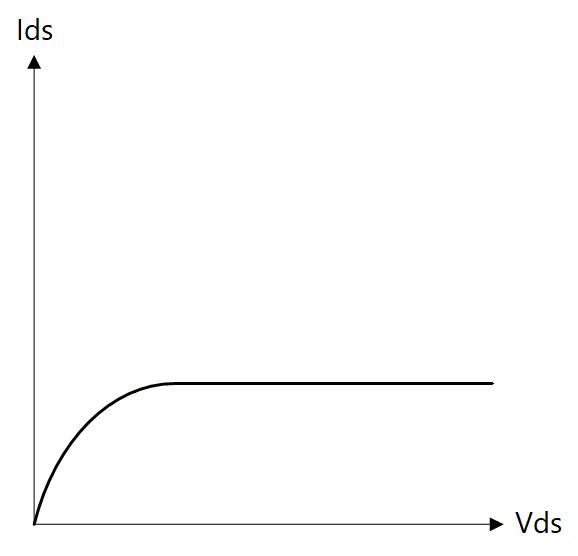
Fig. 3-13
“3極管”、”5極管” というのは真空管時代を引き摺った呼び方です。 実はバイポーラトランジスタでは 3極管領域を “飽和領域” と呼び、MOSトランジスタでは 5極管領域を “飽和領域” と呼ぶため、紛らわしいので、私は 3極管・5極管という呼び方に統一しています。
MOSトランジスタのみしか扱わない場合は紛れはないので、最初から線形・飽和と呼んだほうが良いかもしれません。
ちなみに、歴史的に先にできたのが 3極真空管で、その改良として 5極真空管が誕生したという経緯があります。 3極管はグリッド電圧とプレート電圧のどちらを変えても電流が変化し、5極管はプレート電圧を変えても電流は変化しません。
※ https://our-house.jp/3kyoku5kyoku/
MOSトランジスタの電気特性
MOSトランジスタの平面図と断面構造図
下に、N型MOSトランジスタとP型MOSトランジスタのレイアウト図と断面構造図を記します。 今までは電子をキャリアとするN型MOSトランジスタで説明をしてきましたが、ほとんどの半導体プロセスでは正孔をキャリアとするP型MOSトランジスタと合わせて、相補型MOS (CMOS)トランジスタを扱います。
L をチャンネル長、Wをチャンネル幅と呼び、印加する電圧以外に、W/L の比率を変えるとそれに比例して電流は増減します。
なお、これまで基板 (Body) 電圧は基板の下側から与えるような図で説明してきましたが、実際の集積回路では下図のように表面側から与えます。
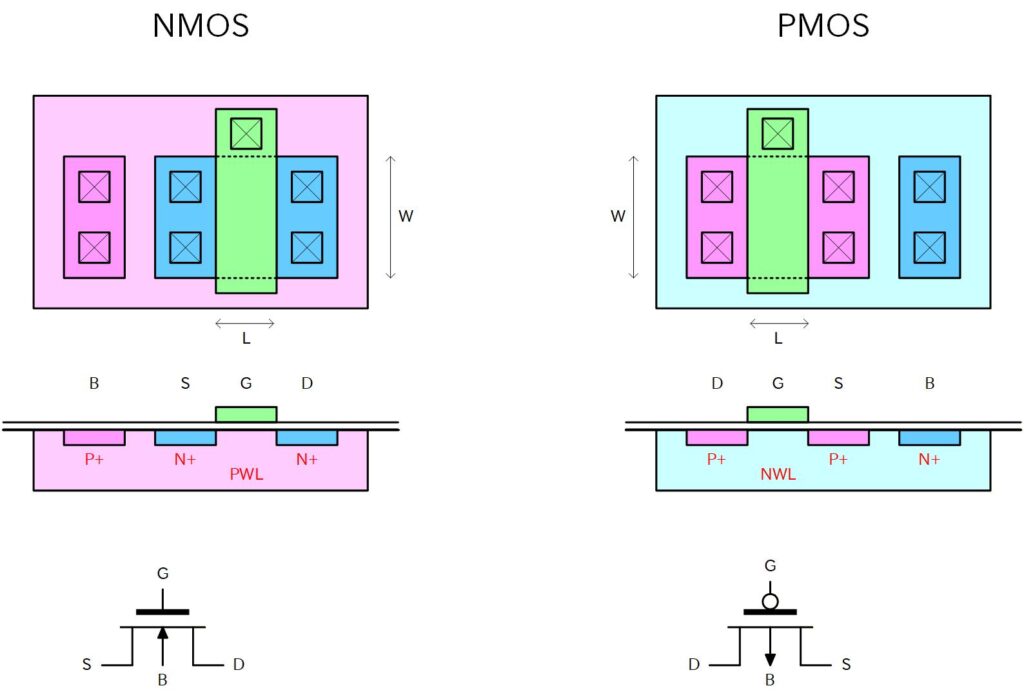
Fig. 4-1
各動作領域における電流の近似式とパラメータ
MOSトランジスタにおける電流の式を理論的に導くことは可能ですが、「アナログ回路設計のためのデバイスの基礎」という講座の趣旨から逸脱しますので、ここでは結果のみを記します。
5極管領域での は
3極管領域での は
5極管条件は
このときの境界となる を と定義すると、5極管条件で使うためには とする必要があります。
また、Gate に実効的に印加される電圧として を定義します。 になるまではトランジスタはオンしないので が を超えた上澄み分、すなわち とします。
これを用いて上記の式を書き換えると 5極管領域の式は
3極管領域の式は
となります。
ここで、 はキャリアの移動度で、電子の場合は 正孔の場合は 程度の値を取ります。 (製造プロセスに依存します)
は酸化膜容量で、 で表されます。 は微細化とともに薄くなり、 は大きくなって微細化により電流駆動能力は上がってきてます。
W, L は Channel の幅と長さで、L は短く、Wは広くすると電流が大きくなります。
は Source を基準としたときの Gate 電圧で、 は Source を基準としたときの Drain 電圧です。
は先に述べたしきい値電圧で、 はこの を超えるまでは動作に寄与しません。 を超えた分の電圧が実効電圧として寄与するため、 を実効電圧 () と呼びます。
は飽和 Drain 電圧のことで、 以上の を印加すると が飽和する 5極管領域になり、それより低い の場合には 3極管領域で動作します。 古典的な近似では は と等しくなります。
の式を で偏微分すると、相互コンダクタンス() が得られます。
これは を微小変化させたときの の変化の割合を示すパラメータで、アナログ回路設計においては極めて重要なパラメータです。
通常は は高い方が有利です。
の式は 5極管領域と 3極管領域で異なるため、それぞれ異なります。
5極管での は
3極管での は
となります。
の式を で偏微分すると、自己コンダクタンス() が得られます。
これは を微小変化させたときの の変化の割合を示すパラメータですが、アナログ回路設計においてはこの逆数をとった Drain 抵抗() の方が一般に使われる重要なパラメータになります。
MOSトランジスタをスイッチとして使う場合は は大きい方がオン抵抗 ()が下がるので有利になりますが、通常は は低く、すなわち は高い方が有利です。
Ids の式は 5極管領域と 3極管領域で異なるため、 () はそれぞれ異なります。
5極管での は
であり、 ということは となります。
3極管での は
となります。
以上の結果から、5極管領域における , と、3極管領域における , の関係を考えます。
5極管領域で を求めると、
一方、3極管領域の を求めると
となり、両者は等しくなります。 このことは と の和は3極管でも5極管でも同じで、3極管で使うと に取られる分 が小さくなることを意味します。
で考えると、3極管で使うと 5極管で∞だった がある有限の まで小さくなることを意味します。
アナログ回路ではスイッチとして使う以外は、MOSトランジスタの , はともに大きい方が有利なのですが、3極管で使うと , はともに低下するため、非常に不利になります。
一般的にアナログ回路では が高く、 も高い 5極管領域で使用することがほとんどです。 例外は MOSトランジスタをスイッチとして使う場合で、この場合のみ 3極管領域で使用することになります。 スイッチにより Source と Drain が完全に導通状態になると となり、その時の をオン抵抗と呼びます。
gm と Veff の関係
5極管領域での と の関係を調べます。
は先に述べたように以下の式で表されます。
は に比例し、W/L 比 を 2倍にすると 2 倍になることがわかります。
5極管の電流の式を について整理して、の両辺の平方根を取ると
は を 2倍にすると √2 倍に、W/L 比を 2倍にすると 1/√2 倍になることがわかります。
また、以上のふたつの式から、
が得られ、 は を 2倍にすると √2 倍に、W/L 比を 2倍にすると √2 倍になることがわかります。
一般に を大きくすると高い が得られますが、 なので、飽和 Drain 電圧が上がり、5極管で使えるいわゆる “美味しい部分” が減ることになり、トレードオフの関係になります。 電源電圧にもよりますが、 としては 0.15〜0.3V 程度が妥当です。
短チャンネル効果と rds
近似式を用いると Fig. 4-2a のような 特性となり、5極管領域では すなわち となりますが、実際には Fig. 4-2b のように曲線は傾きを持ちます。 すなわち は有限の値を取ります。
この理由は短チャンネル効果と呼ばれるもので、Drain と P-sub との間にできる空乏層幅が変化することによります。
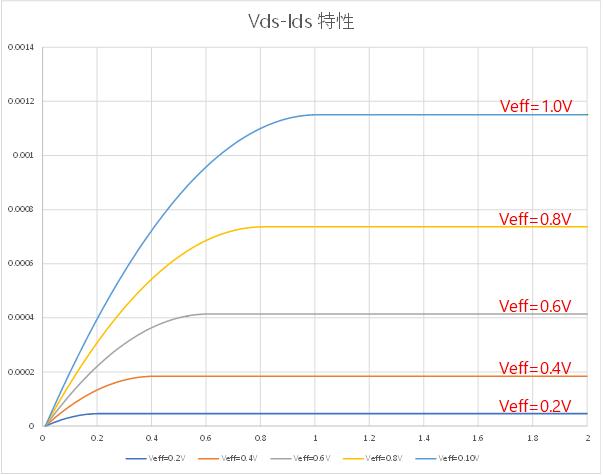
Fig. 4-2a
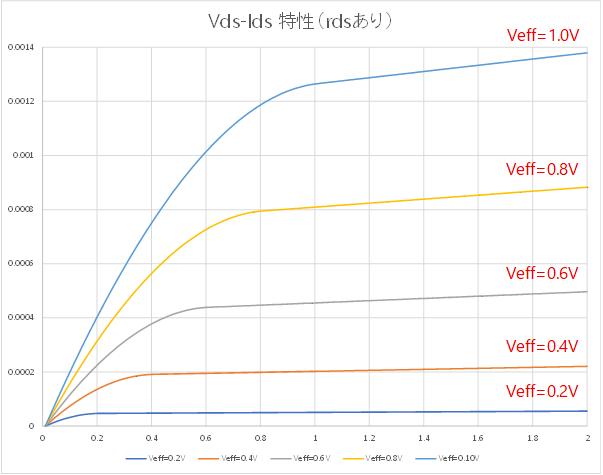
Fig. 4-2b
Fig. 4-2
Drain は N型で P-Sub は P型なので、Fig. 4-3 に示すように空乏層ができます。
Soource から注入された電子がこの空乏層まで達すると、空乏層内の電界で加速されて Drain へ排出されます。
なので実効的なチャンネル長というのが、Source 端から Drain空乏層端までの長さになります。
ここで、Drain と P-Sub との間にできる空乏層の幅は逆バイアス電圧に依存し、Drain電圧が高くなるほど空乏層は広がり、実効チャンネル長が短くなって電流が増えることになります。
これを短チャンネル効果と呼び、ゲート長の短い微細化プロセスになると顕著になり、極端な場合は空乏層が Source 端まで延び、Source と Drain が短絡状態になる、いわゆるパンチスルーが発生します。 このため微細化プロセスになると Drain 電圧を下げる必要が出てきます。
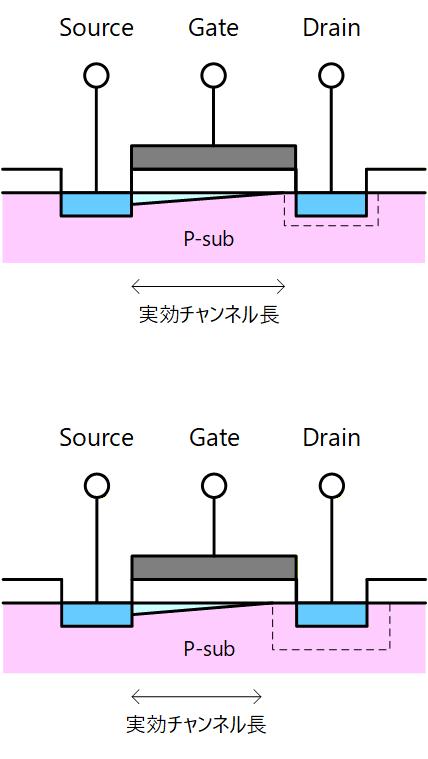
Fig. 4-3
バックゲート効果と Vth シフト
これまでの説明ではMOSトランジスタの電流は Vgs, Vds で記述され、P-sub の電位には関係ないように見えていましたが、P-sub の電位を高くすると Vth が大きくなるという、いわゆるバックゲート効果というものがあります。 (Gate が正門なら Body は裏門に相当することから Body をバックゲートと呼びます)
通常は Vbs=0V で使いますが、この後の講座で説明するソースフォロワや、差動対などではバックゲート効果が影響してくる場合があります。
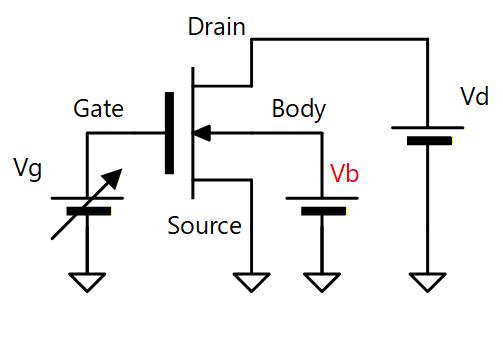
Fg. 4-4a
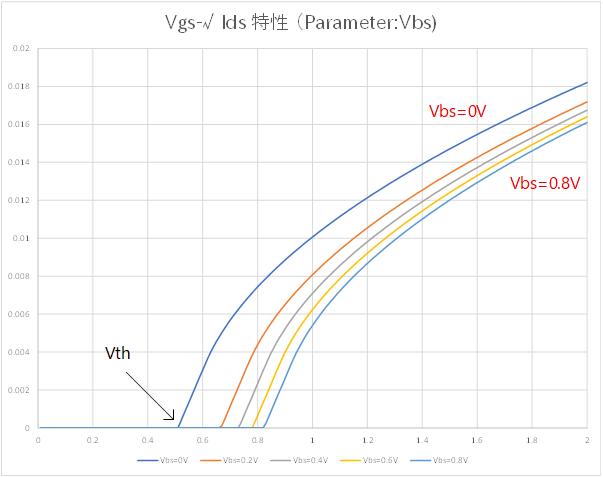
Fig. 4-4b
Planner プロセスではこのバックゲート効果は無視できないほど大きく、Vth シフトを避けるために”ホットウェル” という手法をよく使ってました。 P-sub の場合には分離された N-Well 上に形成された PMOS に対して使える手法です。 近年の fin-FET プロセスでは、バックゲート効果はほとんど無いのが特徴です。
MOSトランジスタにおける容量
MOSトランジスタでは、各端子間には容量が存在し、それらはトランジスタがどの領域で動作しているかに応じて異なります。
まず、Source と Body、および Drain と Body の間には接合容量が存在します。 これはそれぞれの端子間の電位差によって変わります。それから Gate と Source、および Gate と Drain の間に、Cgs0, Cgd0 と呼ばれる容量があります。 MOSトランジスタでは電流駆動能力を稼ぐため酸化膜厚は薄くしますが、そうすると Source, Drain の端部で薄い酸化膜を介した並行平板コンデンサができるためです。
以上の容量は動作領域に依存しませんが、以下では動作領域に依存する容量について説明します。
遮断領域
遮断領域では Gate と Body の間に、酸化膜容量と空乏層容量の直列接続容量ができます。
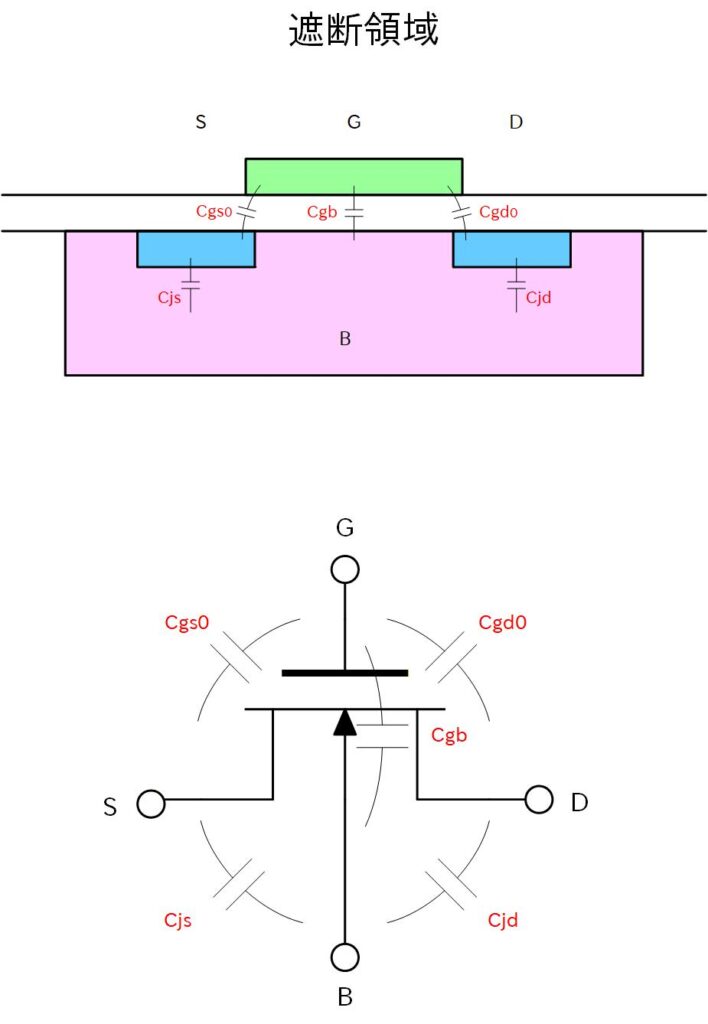
Fig. 4-5a
3極管・5極管領域
Gate電圧が Vth を超え、Channel に反転電子が誘起されると、Gate からは Channel との間の酸化膜容量が見えてきます。
Channel の電子は Source と Drain のどちらとも電気的に接続されるため、3極管では Cox を半々に分け合う形となり、5極管では Source側に の容量を、Drain側とは容量を持たないように振る舞います。 これはDrain の周りには空乏層があるため、チャンネルの電子とは切り離されるためです。
一般に、接合容量より酸化膜容量が大きいことと、アナログ回路では 5極管動作で使うことから、もっとも支配的な容量は Gate-Source 間のチャンネル容量になります。
ただし、後の講座で解説する、インバータのミラー容量というものがあり、これには Gate-Drain の結合容量である Cgd0 が効いてきます。
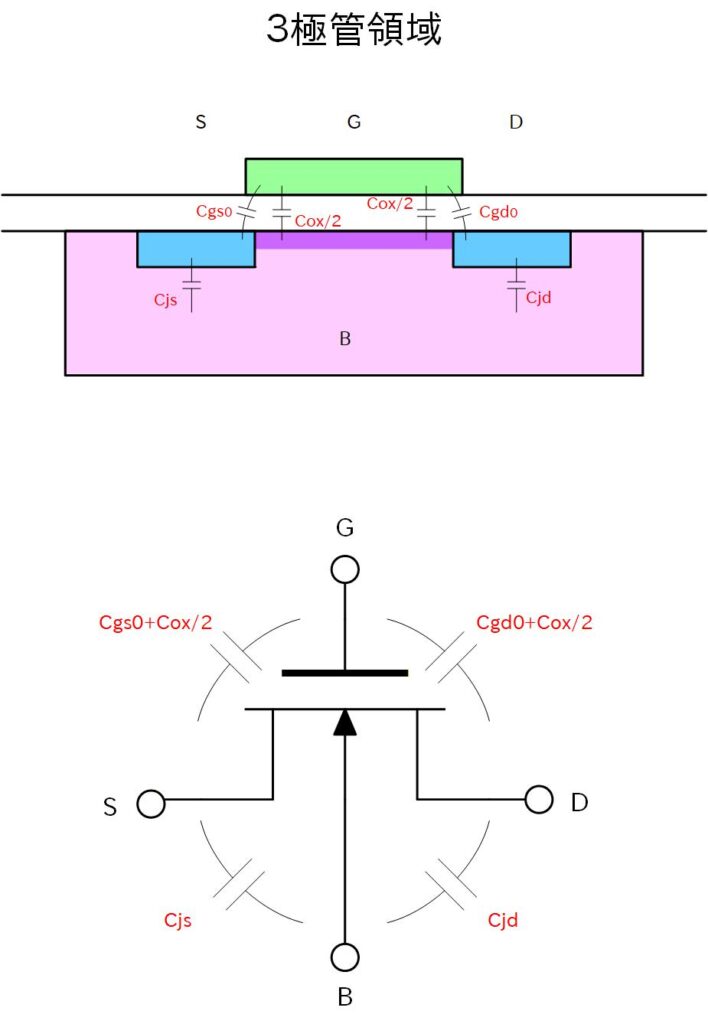
Fig. 4-5b
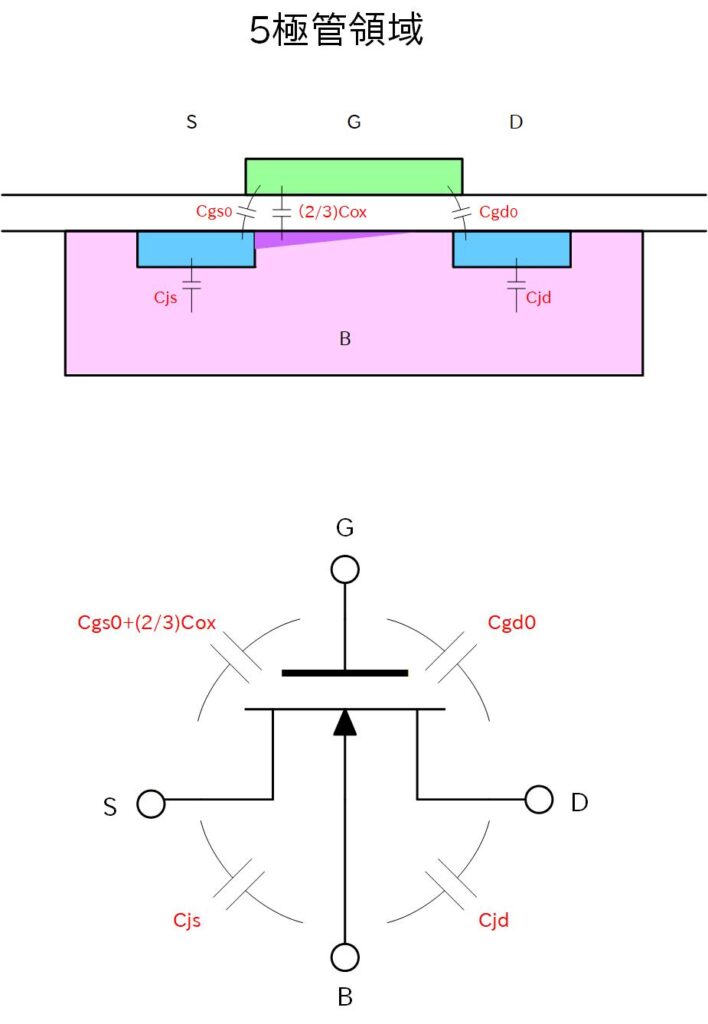
Fig. 4-5c
まとめ
以上、バルクの半導体から始まり、PN接合容量、MOS トランジスタの原理や動作などを解説してきましたが、アナログ回路設計という観点からはこれらを全て完全に理解する必要はありません。
ただデバイスの構造まで把握していると、例えば動作帯域を上げるためにどこの容量を抑えればよいか、そのためにはレイアウトのここに注意が必要などという、一歩進んだ設計ができるのではないかと私は思います。



コメント