定電流源
理想定電流源とは
定電流源とはその名前の通り、一定の電流を流す素子です。
理想的には端子の電圧に関わらず所定の電流を流す素子で、小信号的には分母の電流の変化量がゼロなので出力抵抗が∞となります
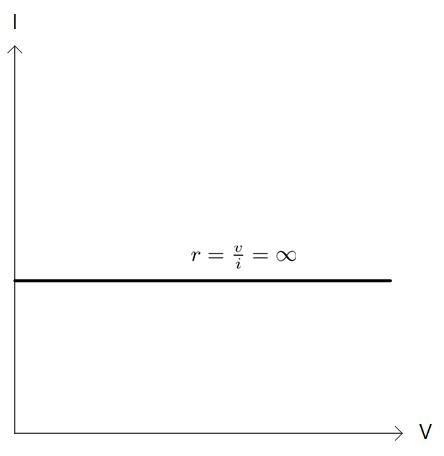
Fig. 1-1
MOS トランジスタによる電流源
MOS トランジスタが 3極管領域で動作しているときには は に依存して変化するため定電流とみなすことはできませんが、5極管領域で動作している場合には基本的に を変えても は変わらないため、定電流源として扱うことができます。
ここで、基本的にと言ったのは、小さいながらも は傾きを持っため、その逆数である が無限大にはならないためです。
MOS トランジスタを定電流源として使用する場合には、理想定電流源に近づくように を極力大きくする必要があります。
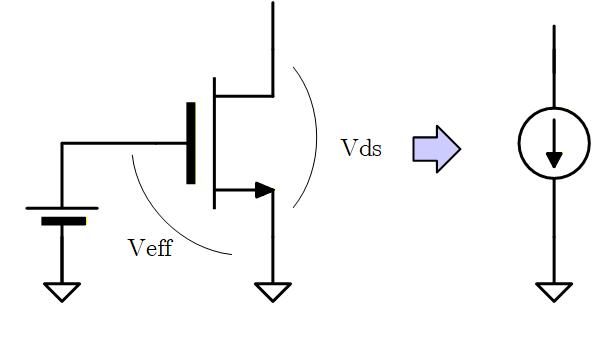
Fig. 1-2
以上から、MOS トランジスタを定電流源として使うためには、
① 5極管で使う
② は大きくする
ことが必要となります。
なお、 を大きくすると小さなサイズで電流は流せますが、
も大きくなるため定電流とみなせる範囲が狭くなります。
また、トランジスタの L を小さくすると電流は流せますが、 は小さくなってしまいます。
一般的に、MOS トランジスタを定電流源とした使う場合は、 は浅めに設定して定電流とみなせる範囲を広くとり、L は長めに設定して を大きくします。 電流を大きくする時は W を広くして対応することが多いです。
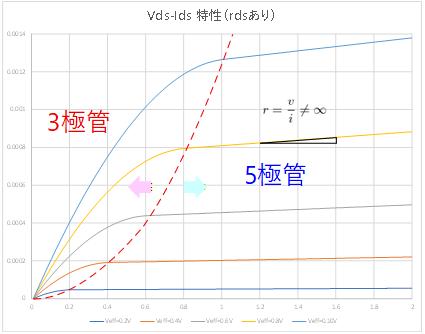
Fig. 1-3
MOS トランジスタは基本的に Source, Drain, Gate, Body の、4端子デバイスですが、Body はほとんどの場合 NMOS はグラウンドで、PMOS は電源電圧になるため、Fig. 1-2 のように Body を省略して 3端子デバイスで書くことが多いです。
Body にグラウンドまたは電源電圧以外の電圧を接続する時のみ 4端子で書き、Bodyの接続先を明示します。
カレントミラー
ダイオード接続
MOS トランジスタの Source を接地し、Drain と Gate を接続したものを ダイオード接続と呼びます。
このダイオード接続の Drain (= Gate) に なる電流を流し込んだときの (=) を調べてみます。
電流を無理やり流そうとすると、その電流を流すようにトランジスタが自動的にバイアスされます。 つまり、その電流が流れるための Gate 電圧が一意に決まります。
また、 で なので となり、 であれば確実に となって、5極管条件を満たすことが分かります。
5極管条件の式は
なので、 を与えたときの は以下の式で与えられます。
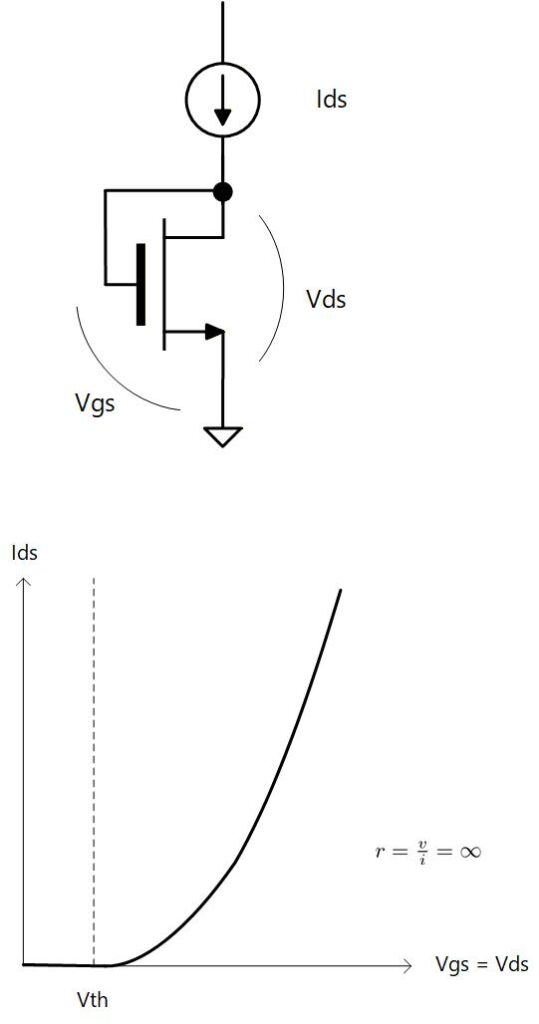
Fig. 2-1
カレントミラー
前節のダイオード接続トランジスタに、サイズの等しいもう一つのトランジスタを追加し、Gate 同士を互いに接続した場合を考えます。
ダイオード接続トランジスタの Gate-Source 電圧を とすると Drain-Source 電流は以下で表されます。
追加したトランジスタの Gate-Source 電圧を 、Drain-Source 電流を とし、このトランジスタを 5極管条件で使うとすると、電流は以下で表されます。
と は等しいので、 と も等しく、追加したトランジスタは、ダイオード接続に流した電流と同じ電流を流すことができる定電流源として使えることが分かります。
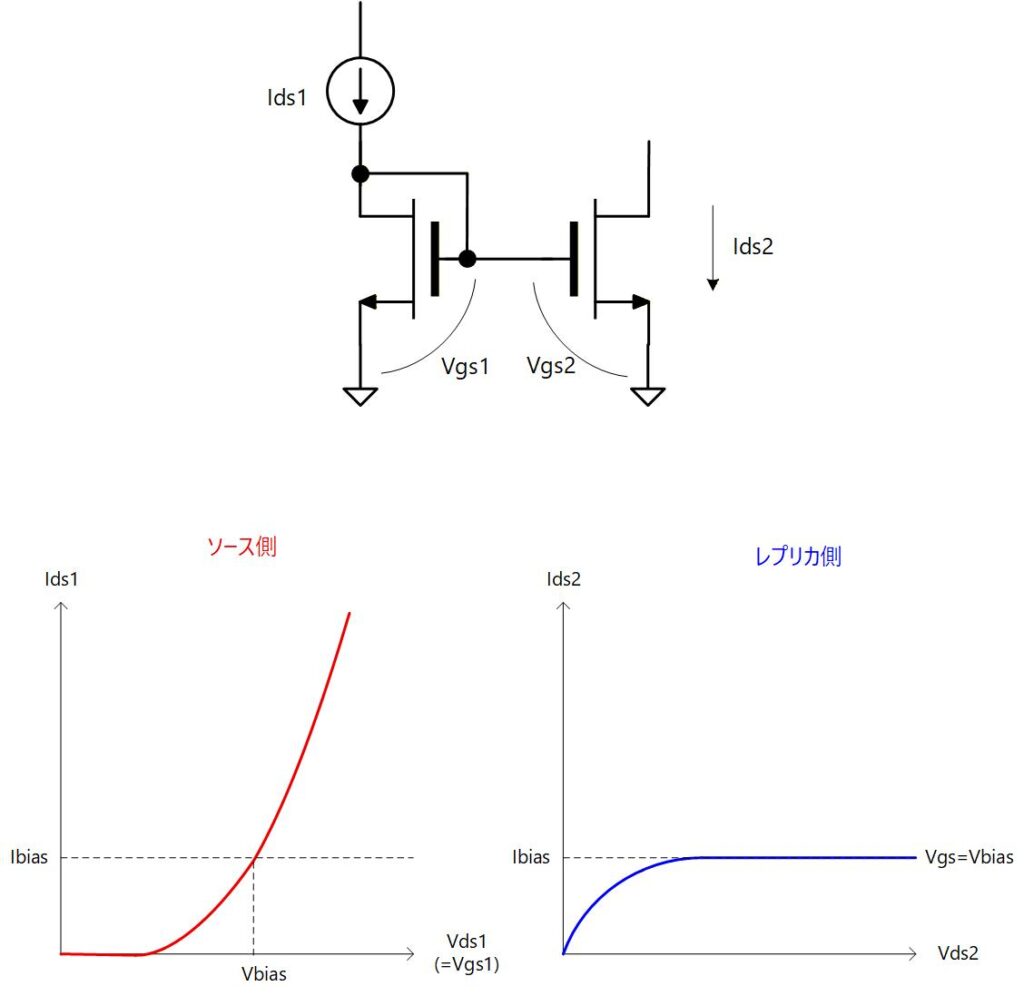
Fig. 2-2
ダイオード接続トランジスタをソース側、追加たトランジスタをレプリカ側と呼ぶと、ソース側に流した電流と同じ電流をレプリカ側で複製できるということになります。
これをカレントミラーと呼びます。
以上、ソース側とレプリカ側とのサイズが同じ場合は単純な複製ですが、例えばレプリカ側のトランジスタの W をソース側の W の 2倍にすると、レプリカ側はソース側の 2倍の電流を流す電流源になります。
また、ソース側で発生させた を複数のトランジスタに供給して、複数のレプリカを作ることも可能です。
このようにカレントミラーは、種となる電流源があれば、それを任意の倍率でいくつでも複製できるので非常に重宝で、アナログ回路には欠かせない重要な回路要素です。
ソース側のバイアス電流を係数倍してレプリカ側に流す場合は、W や L を変えても理屈の上では OK なのですがあまり好ましくはなく、トランジスタの数を変えるのが一般的です。 例えばソース側を 2個のトランジスタで構成し、レプリカ側を 1個のトランジスタにすればソース側の 1/2の電流が、レプリカ側を 4個のトランジスタにすればソース側の2倍の電流が得られます。
上の説明ではソース側とレプリカ側で Source 電位はともにグラウンドとして共通としてますが、実際の集積回路ではグラウンドのメタル配線は有限の抵抗を持ち、そこに電流が流れると電位降下が発生しますので、グラウンド電位が場所によって異なることが多いです。 その場合には Gate 電位が等しくても Source 電位が異なるので両者の にズレが生じます。 そうなると正しく電流複製ができなくなるので注意が必要です。
インバータ (ソース接地)
MOS トランジスタの Source を接地し、Gateを入力、Drain に負荷を接続した回路をインバータと呼び、ソース接地接続とも呼びます。
ここで接地と言っているのは DC的にグラウンドに接続しているということではなく、AC的に電圧が変わらない、小信号接地を意味します。
以下、負荷として ①抵抗、②定電流源 の 2つのパターンについて説明します。
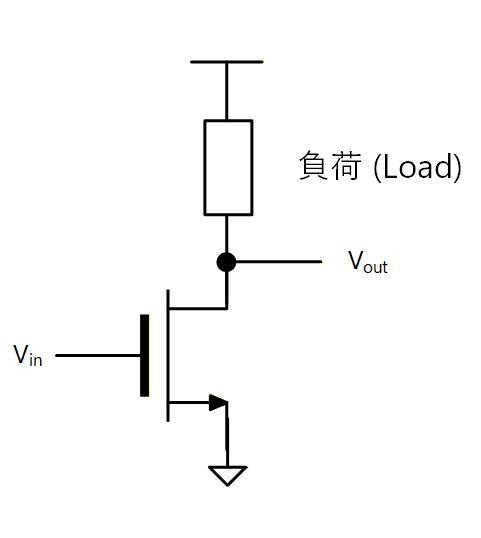
Fig. 3-1
抵抗負荷
負荷として抵抗を用いた場合、トランジスタを流れる が抵抗にも流れるため、電位降下効果により の電圧は から だけ下がった電圧になります。 よって は と表されます。
ここで、 でもあるので となり、トランジスタの 特性のグラフに書き込むと赤の直線になります。 これを負荷直線と呼びます。
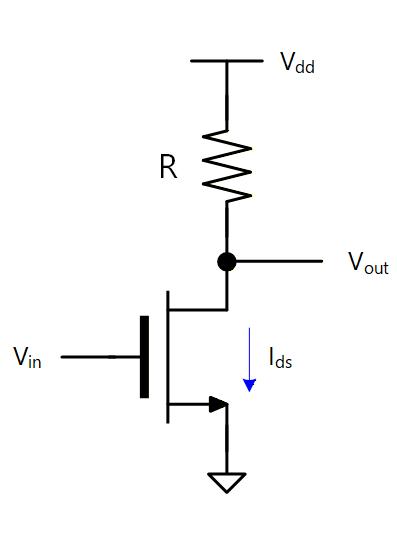
Fig. 3-2
Gate 電圧、すなわちインバータの入力電圧 を 0 から上げていく場合を考えます。(Fig. 3-3)
の範囲ではトランジスタは遮断状態のため で、負荷抵抗には電位降下は発生せず、 となります。
そこから を上げ、 になるとトランジスタは 5極管領域で動作を始めて、 によって とともに が増加するため、負荷抵抗における電位降下は大きくなり、 は下がり始めます。
さらに を上げるとトランジスタは 3極管領域に入り、 が下がり始めるため、 の増え方は小さくなります。 すなわち に対する の変化率が下がります。
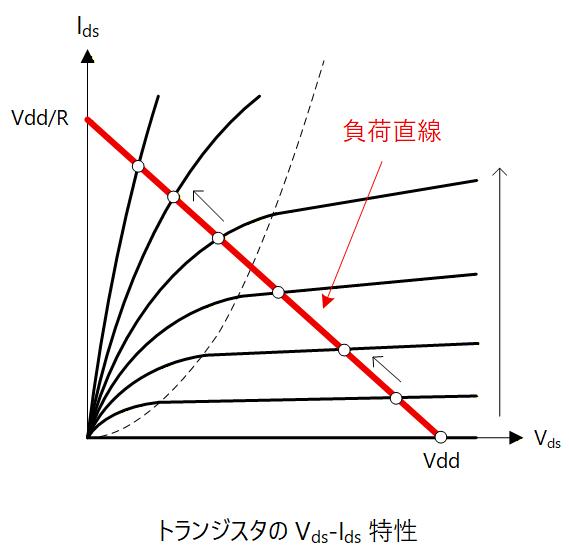
Fig. 3-3
この振る舞いを入力電圧に対する出力電圧のグラフとして表すと、 Fig. 3-4 のようになります。
に対する の変化率を入出力ゲインと呼び、アナログ回路で使用するインバータはゲインの高い 5極管領域で使うことが一般的です。
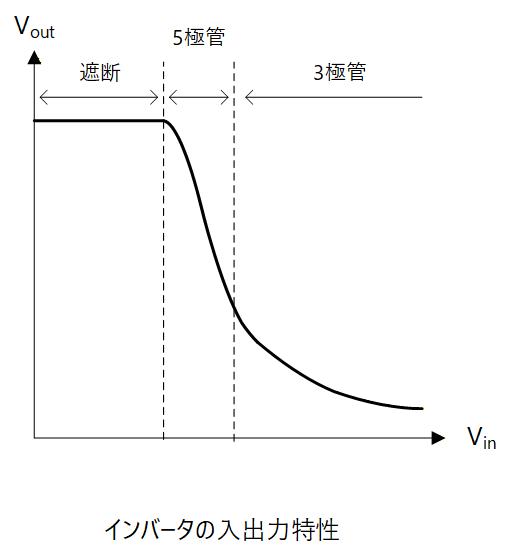
Fig. 3-4
次にインバータのゲインを小信号等価回路で求めてみます。
トランジスタは に応じて流れる電流が変化する電流源と、 に応じて流れる電流が変化する抵抗が並列接続されたものとして表すことができます。(Fig. 3-5 上図)
は小信号的には変化しないので接地と等価になり、Fig. 3-5 下図のように書くことができます。
ここで、
であり、キルヒホッフの法則から、 なので
これを変形すると
が、得られます。
は数100kΩ〜数MΩのオーダーで、R を数 kΩ 程度とすると、通常は なので、ゲインは となります。 を 数mMho 程度に取ると、ゲインは概ね 10〜20dB 程度になります。
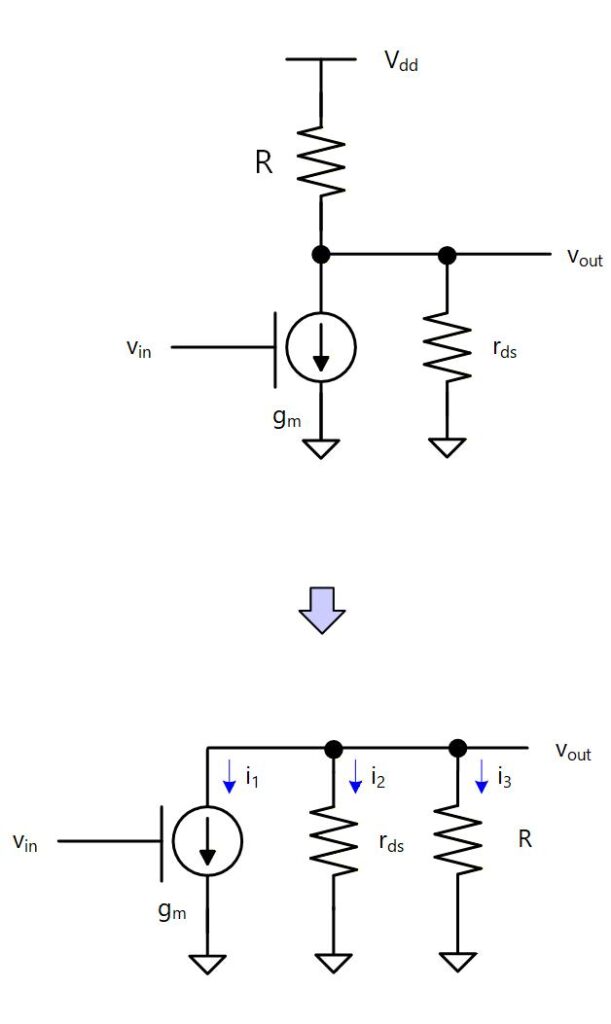
Fig. 3-5
小信号解析の場合には、信号は小文字で書き表わすのが慣習です。
電流源負荷
ここでは電流源としては理想定電流源ではなく、MOSトランジスタを用いた場合について説明します。
PMOS カレントミラーを構成して、所定の電流を流しますが、Drain 電圧は 電圧から までは 3極管で動作し、Drain 電圧が より下がったら 5極管領域に入り、定電流源として働きます。
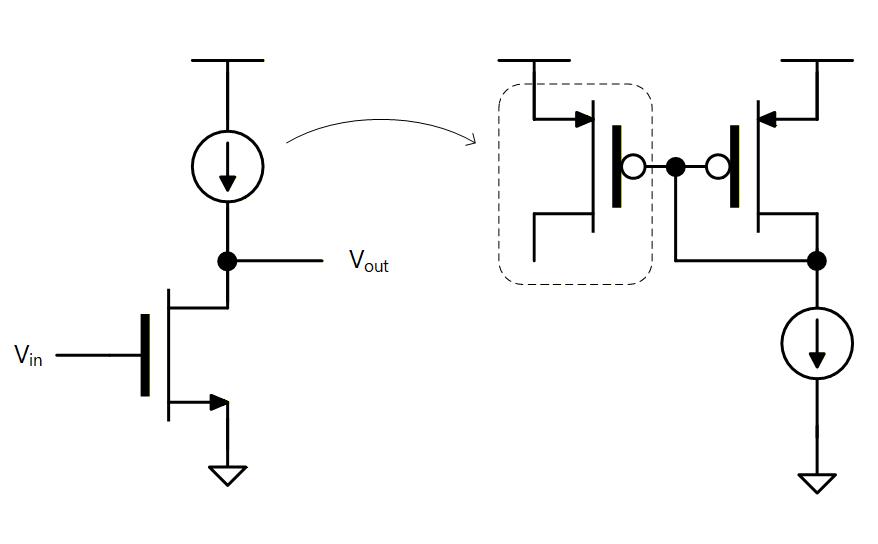
Fig. 3-6
Fig. 3-7 に、トランジスタの – 特性のグラフに PMOS 電流源による負荷曲線を追加した図を示します。
この図で、 すなわちインバータの入力電圧 を 0 から上げていく場合を考えます。
の領域ではトランジスタは遮断状態のため で、PMOS電流源にも電流は流れないため、 となります。
そこから を上げ、 になるとトランジスタは 5極管領域で動作を始めますが、電流源 PMOS がまだ 3極管領域にいるので は緩やかにしか下がって行きません。
電流源 PMOS が5極管に入るとトランジスタの負荷は定電流源になり、ここでは が僅かに変化しただけで は一気に下がります。 すなわちに に対する 変化が大きい、すなわち高ゲインが得られます。
このあとは を上げると NMOSトランジスタが 3極管領域に入り、 が下がり始めるためゲインは落ちてきます。
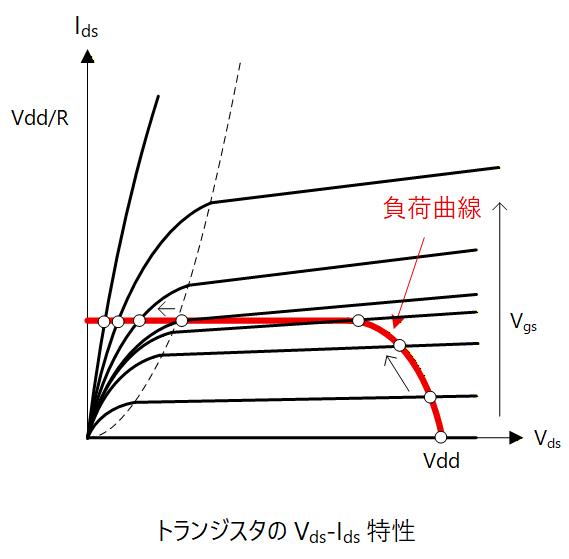
Fig. 3-7
この振る舞いを入力電圧に対する出力電圧のグラフとして表すと、 Fig. 3-8 のようになります。
5極管領域は rds ご高く、僅かな電流変化でも電圧の変化は大きくなります。 なので、PMOS, NMOS ともに 5極管動作する領域では に対する 入出力ゲインが極めて高くなります。
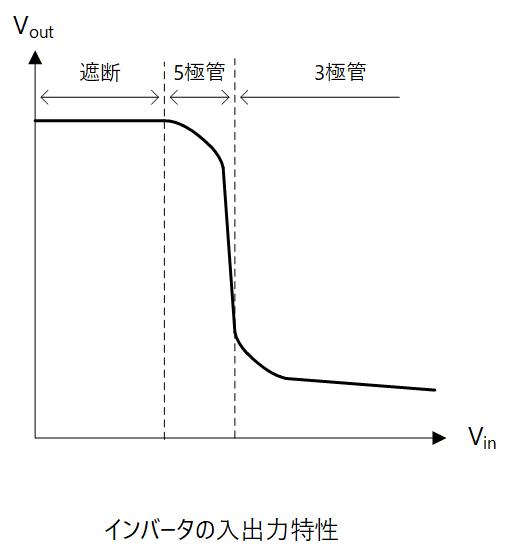
Fig. 3-8
ゲインが高いということは使える 範囲が非常に狭いということを意味します。 その場合には高ゲインの美味しいところで使うのが難しいと感じるかもしれませんが、それはフィードバックをかけて使用することで解決します。
詳細は「フィードバック」の章で解説します。
次にインバータのゲインを小信号等価回路で求めてみます。
前節で述べたように トランジスタは に応じて流れる電流が変化する電流源と、 に応じて流れる電流が変化する抵抗として表すことができ、 は小信号的には変化しないので接地と等価になります。(Fig. 3-9 上図)
このとき、定電流源の出力抵抗を ∞ とみなすと Fig. 3-9 下図のように書けます。
ここで、
キルヒホッフの法則から、 だから
これを変形すると、
は数100kΩ〜数MΩ、 は数mMho なので、ゲインは 30〜40dB と非常に大きいゲインが得られます。
なお、小信号等価から明らかなように、このインバータの出力抵抗は となり、ゲインが高い分だけ出力抵抗は高くなってしまうともいえます。
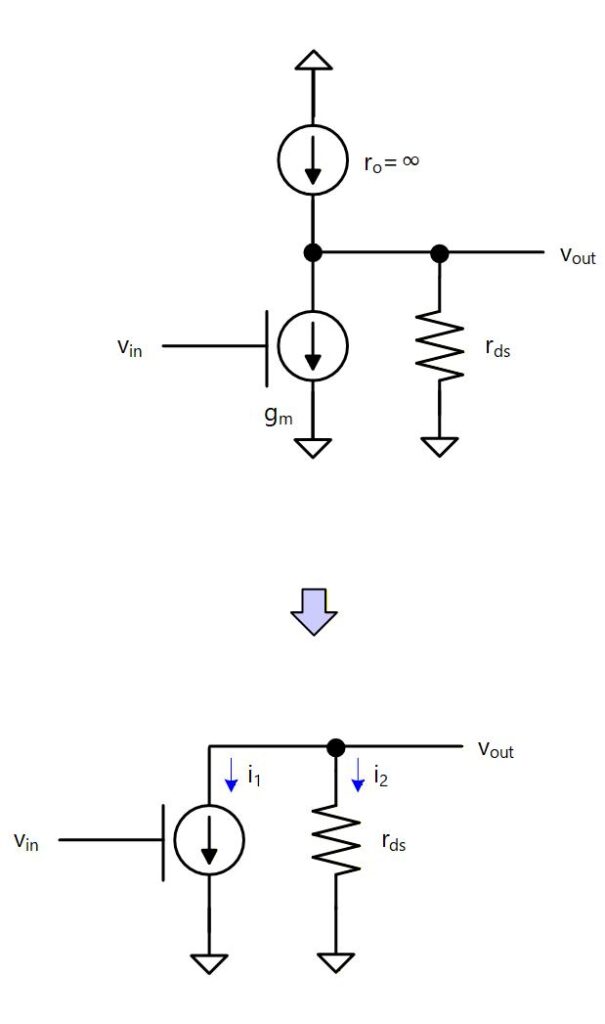
Fig. 3-9
ミラー効果
インバータを使用する際に気をつけなければならないこととして、ミラー効果があります。
「デバイスの基礎」で説明したように、トランジクタの Gate と Drain の間には と呼ばれる容量が存在します。
インバータを構成すると、この容量は入力端子と出力端子の間に存在することになります。
(Fig. 3-10)
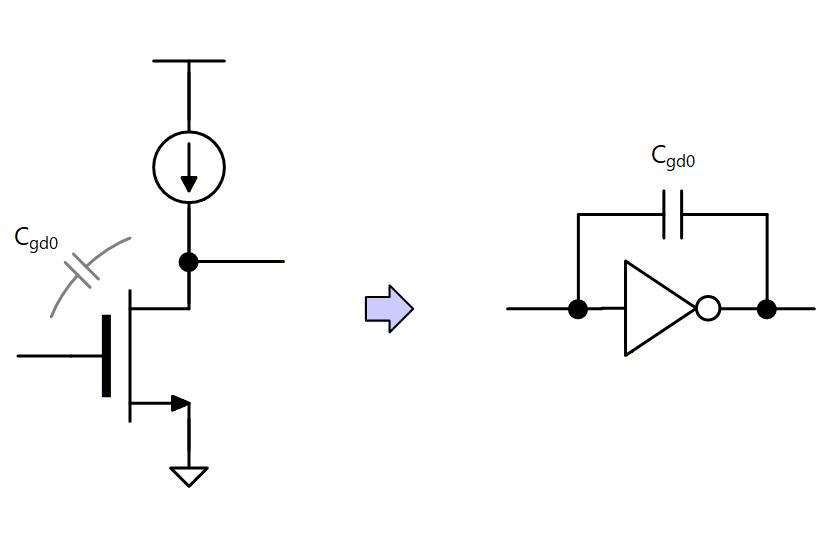
Fig. 3-10
このように、入力端子と出力端子の間に という寄生容量があるインバータに、電圧 で出力抵抗 の電圧源から入力を与えたときの出力を求めてみます。
ここではインバータのゲインを (負号は反転を意味) とします。
ここでインバータの入出力の関係から
抵抗を流れる電流から
容量を流れる電流から
キルヒホッフの法則から、 だから
を代入しね整理すると
ここで とおくと
なので、インバータの応答時定数を決める が実質的にインバータのゲイン倍されることになり、インバータの動作帯域を大きく悪化させることがわかります。

Fig. 3-11
ミラー容量は右図に示したような、固い地面に置いたバケツに水を入れる場合と、底なし沼のように沈み込むような地面に置いたバケツに水を入れる場合のアナロジーで考えると理解しやすいかもしれません。
固い地面に置いたバケツでは入れた水の分だけ水位が上がりますが、沈み込む地面の場合は重さでバケツが沈むため、同じ量の水を入れても地面から見た水位はなかなか上がりません。
つまり必要な水位まで入れるためには大量の水(電荷)が必要ということになります。
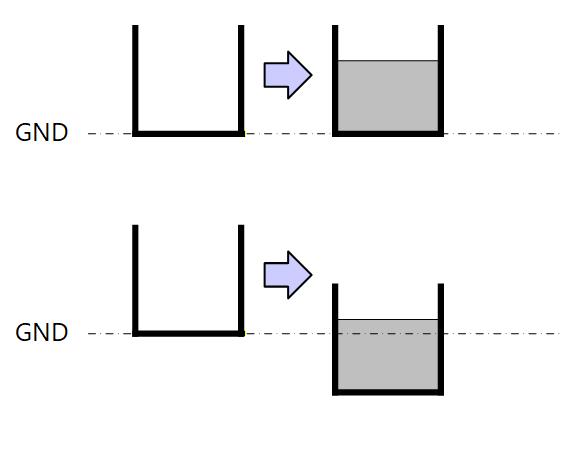
Fig. 3-12
ゲインを落とさずにミラー容量による遅延を低減するためには、信号源の出力抵抗を下げるか、後述するカスコードを利用します。
普段は嫌われもののミラー容量ですが、小さな面積で大きな容量が必要な場合に、積極的に使う場合があります。
ソースフォロワ (ドレイン接地)
MOS トランジスタの Drain を電源電圧に接続し、Gateを入力、Source に負荷を接続した回路をソースフォロワと呼び、ドレイン接地接続とも呼びます。
ここで接地と言っているのは AC的に電圧が変わらない、小信号接地を意味します。
以下、負荷として ①定電流源、②抵抗の 2つのパターンについて説明します。
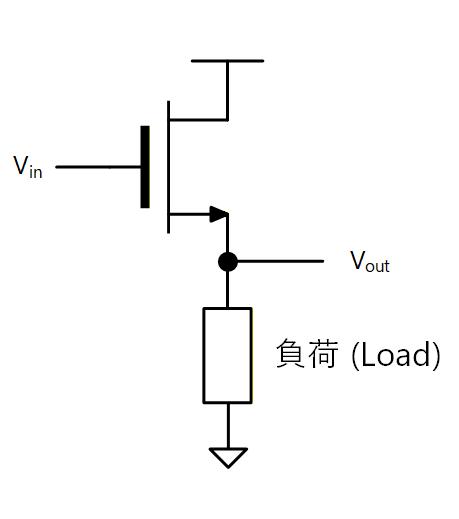
Fig. 4-1
定電流源負荷
負荷として定電流源を与えた場合は、MOSトランジスタにその電流を流そうとします。
このトランジスタを 5極管条件で使うとすると、電流の式は以下で与えられます。
式を変形すると
左辺は Gate 電圧と Source 電圧の差、すなわち と 電圧の差で、右辺は定数項になります。すなわち、 は 電圧を一定の電圧だけレベルシフトした形として表されます。
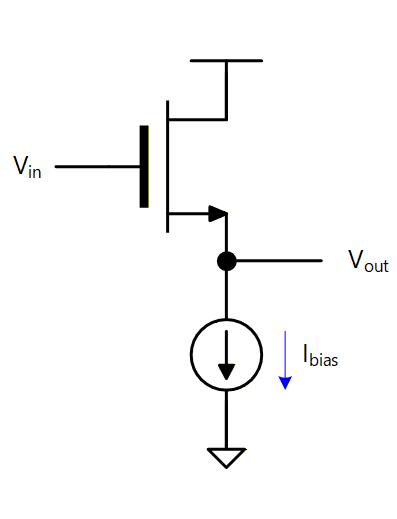
Fig. 4-2
これをグラフで表すと Fig. 4-3 のようになります。
のグラフを 下に平行移動したかたちとなります。
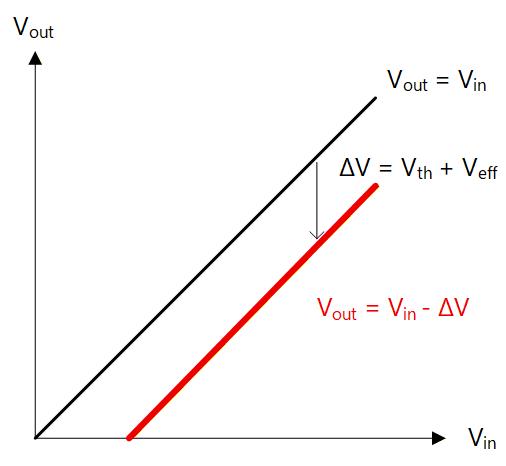
Fig. 4-3
次にソースフォロワのゲインを小信号等価回路で求めてみます。
前節で述べたように トランジスタは に応じて流れる電流が変化する電流源と、 に応じて流れる電流が変化する抵抗として表すことができ、 は小信号的には変化しないので接地と等価になます。 (Fig. 4-4 上図)
ここで、定電流源は出力抵抗は∞となるので Fig. 4-4 下図のように書くことができます。
ここで
定電流源は小信号電流は流れないから、 とみなして
これを変形すると
は一般に 100〜1000 などの非常に大きい値を取るので、分母の は殆どゼロとなって、ゲインはほぼ 1 になることがわかります。
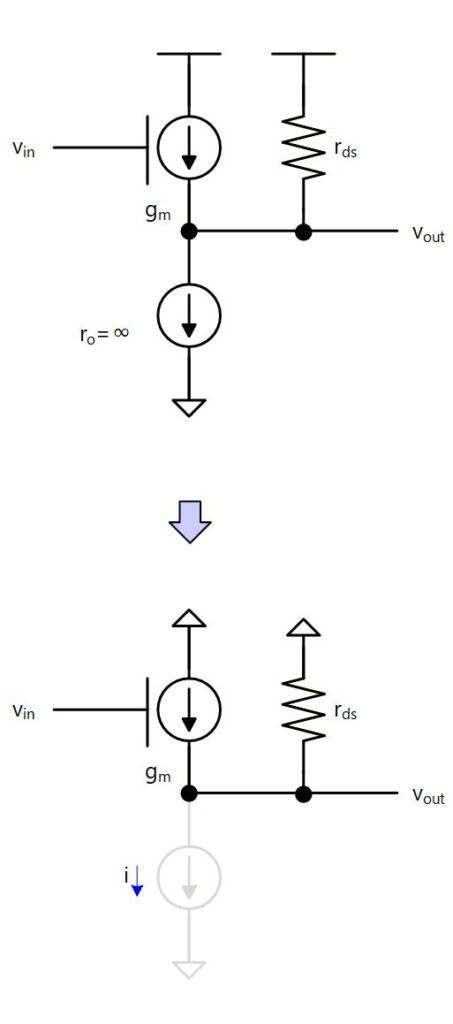
Fig. 4-4
次にソースフォロワの出力抵抗を考えます。 いま を強制的に接地した場合、出力短絡電流は
となります。
一方出力開放電圧 は で、 なので、
すなわちソースフォロワの出力抵抗は とトランジスタの相互コンダクタンスの逆数で与えられます。
は 数100Ω〜数mΩ 程度になるので、ソースフォロワの出力抵抗は 1kΩ〜数kΩ程度の比較的小さな値を取ります。
ソースフォロワは、入力信号を増幅する作用はありませんが、出力抵抗が小さいという特徴があります。
出力抵抗の高い回路の後段において前段の信号振幅はそのままに、出力抵抗を下げるという、いわゆるインピーダンス変換に用いられます。
抵抗負荷
負荷として抵抗をつけた場合の回路図を Fig. 4-5 に示します。
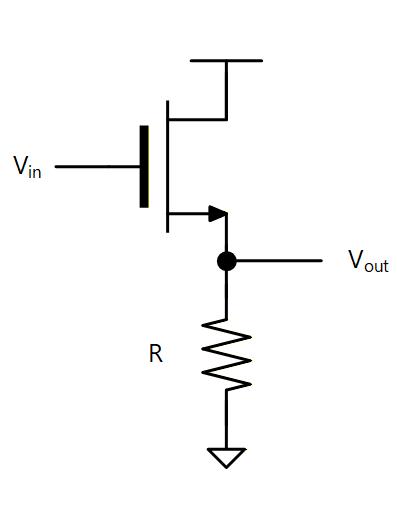
Fig. 4-5
Fig. 4-6 に等価回路を示します。
各小信号電流は
だから
以上からゲインを求めると
だから
分母が 1より大きくなるのでゲインは 1 より小さくなることがわかります。
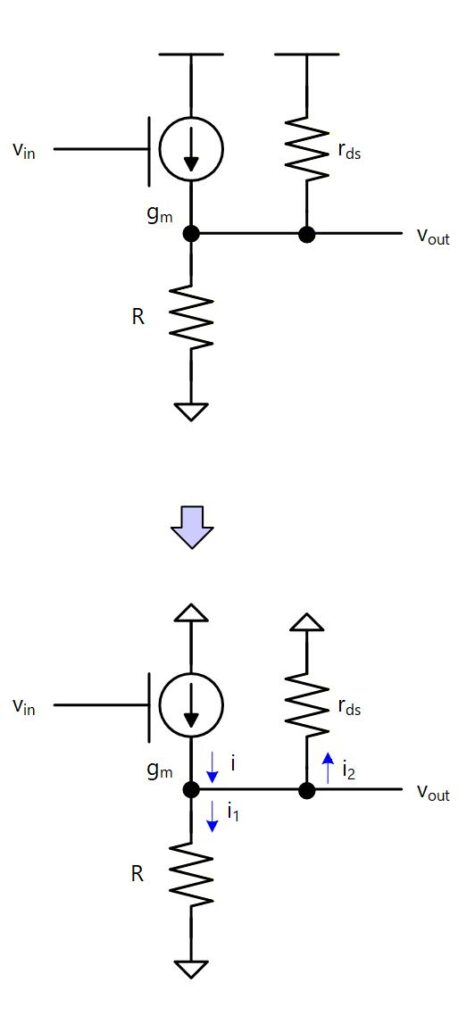
Fig. 4-6
バックゲート効果の影響
これまでの説明ではトランジスタは Body 端子を外した 3端子シンボルで説明してきましたが、実際には NMOS トランジスタの Body は共通の P-Sub に接続され、電位はグラウンドになります。
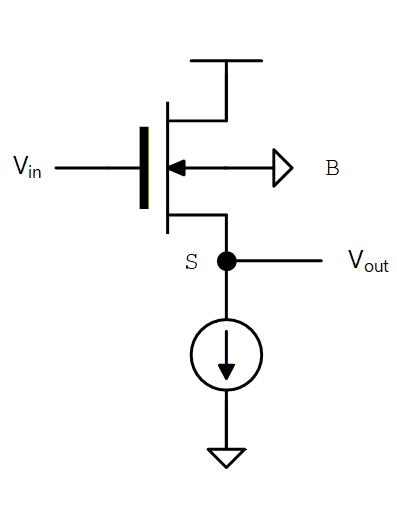
Fig. 4-7
したがって となるようにしたときには、Source を基準にすると Body に の負電圧がかかることになり、バックゲート効果で が高くなります。 このバックゲート効果による のシフト量を とすると
と書けます。
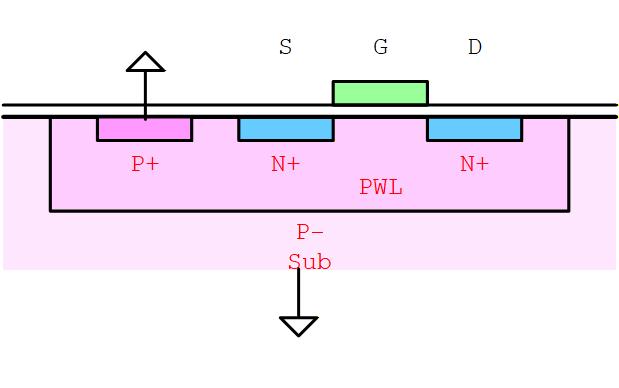
Fig. 4-8
入出力特性をみると、Fig. 4-9 のようにバックゲート効果がない場合に対して、シフト量が 分だけさらに大きくなったようになります。
それだけにとどまらず、ゲインにも影響を及ぼします。
小信号的に言えば、 すなわち が変化すると も変化するため、 も変化して流れる電流 も変化することになります。
に対する の変化率を と表すと、小信号におけるゲインの式は以下のようにかけます。
は 0.1〜0.2 程度の大きさですが、それでも分母にこの項が加わるため、ゲインは 0.7〜0.8 程度と下がることになり、不利な方向に働きます。
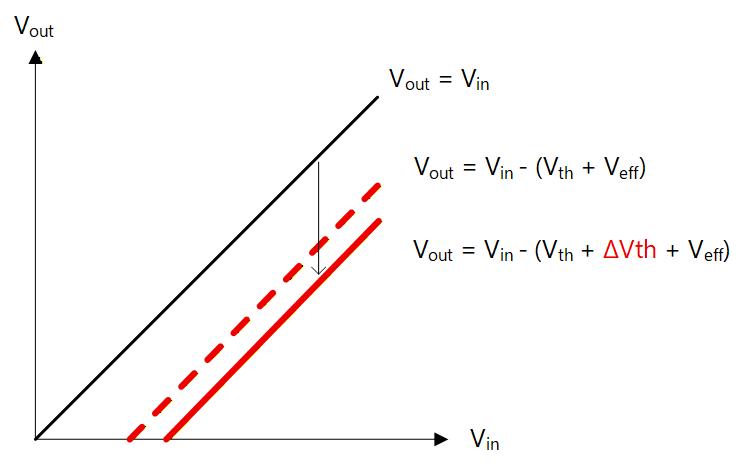
Fig. 4-9
なお、Fig. 4-10 のように PMOS 使ったソースフォロワの場合には、P-sub 上に形成された NWL は、トランジスタごとに異なる電圧にすることが可能なため、 Body を Source に接続することができ、バックゲート効果なしで使うことが可能です。
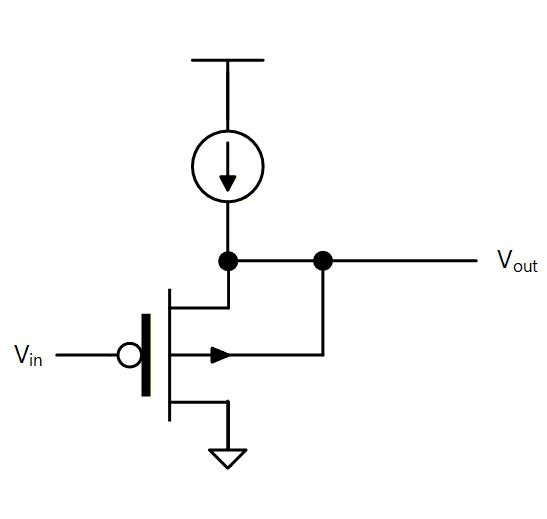
Fig. 4-10
このように Body を Source に接続すると、ウェル電位が動くことになるので、これを「ホットウェル」と呼ぶこともあります。
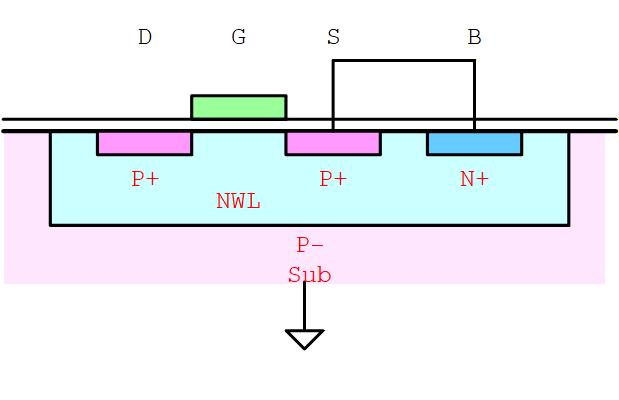
Fig. 4-11
近年のプロセスではトリプルウェル構造もあり、この場合には NMOS でもホットウェルで使用することが可能です。
また、fin FET プロセスでは、そもそもバックゲート効果がほとんどないため、ソースフォロワでゲインが低下する問題は起きません。
カスコード (ゲート接地)
MOS トランジスタの Gate を接地し、Source を入力、Drain を出力とした回路をカスコードと呼び、ゲート接地接続と呼びます。
ここで接地と言っているのは DC的にグラウンドに接続しているということではなく、AC的に電圧が変わらない、小信号接地を意味します。
以下、使い方として ①出力抵抗改善、②ミラー容量低減の 2つのパターンについて説明します。
rds の改善
先に述べたように、電流源はトランジスタを使って実現します。
本来必要なのは理想定電流源ですが、トランジスタを使った場合には によって理想からのズレを生じます。
理想電流源は端子の電圧が変わっても電流は変わりません。
しかし があると、端子の電圧が変わるとそこに電流が流れるため、その分だけ理想電流源からズレることになります。
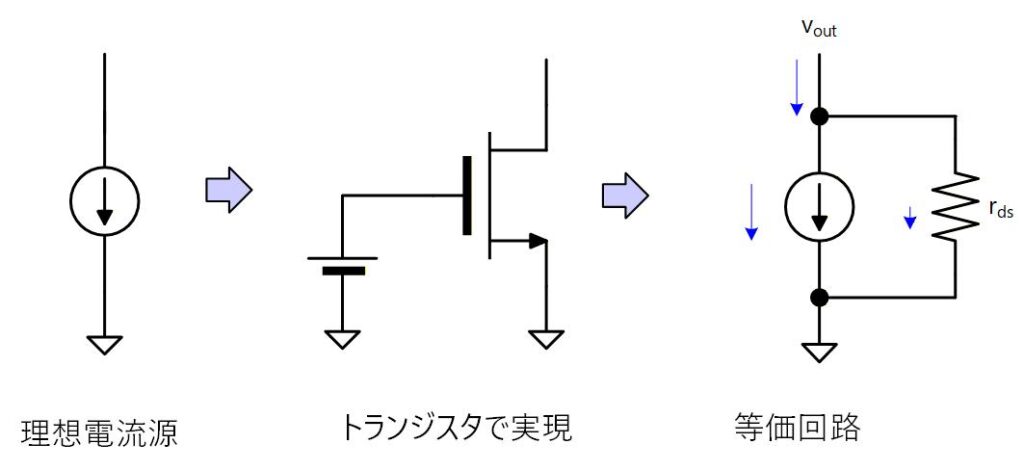
Fig. 5-1
Fig. 5-1 のように、電流源トランジスタの上にもう一つのトランジスタ (カスコードトランジスタ) を追加してみます。
電流源トランジスタの Gate には の電圧を与え、Drain 電圧は電流源トランジスタが 5極管動作するために必要な 電圧以上の を与えるようにカスコードトランジスタの Gate 電位を決めます。
つまり、 となるように を与えます。
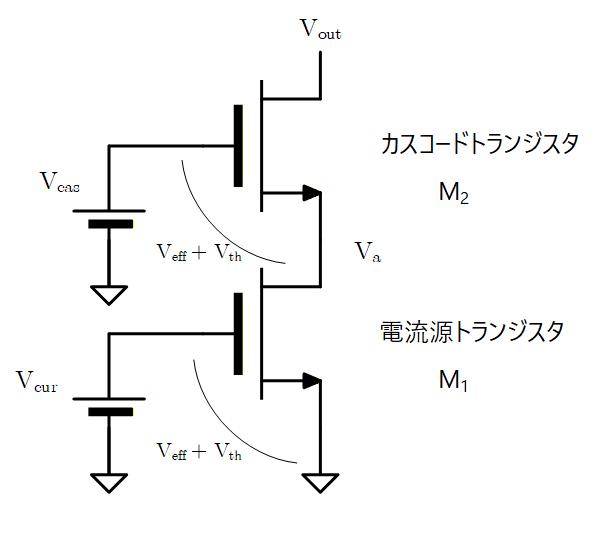
Fig. 5-2a
このバイアス条件で小信号解析を行います。
M1 は Gate 電圧も Source 電圧も AC的には接地なので に起因する電流はゼロで、 に起因する小信号電流のみが流れ、それを とすると、
M2 は Gate 電圧は AC的に接地されているが、Source 電圧は変化するため、 起因と 起因の小信号電流が流れ、これは M1 に流れる小信号電流 と等しいので、
として左辺括弧内の を無視すると になるので、
出力抵抗は だから
カスコードトランジスタがない場合の出力抵抗は で、カスコードトランジスタをいれるとその出力抵抗が 倍に “増幅” されることと等価になります。
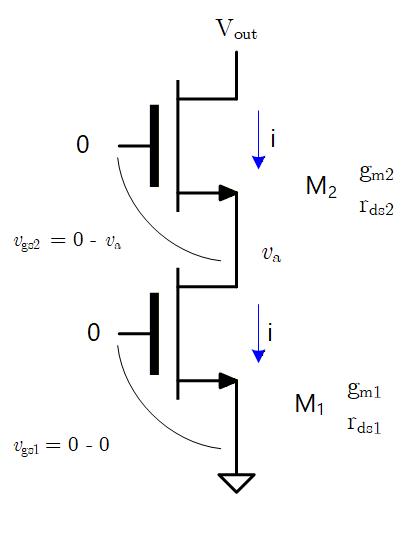
Fig. 5-2b
が数100kΩ程度だったとして、 が 30dB あれば、数10MΩの非常に高い出力抵抗が得られることになり、Fug. 5-2c のように理想電流源に近づけることが可能になります。
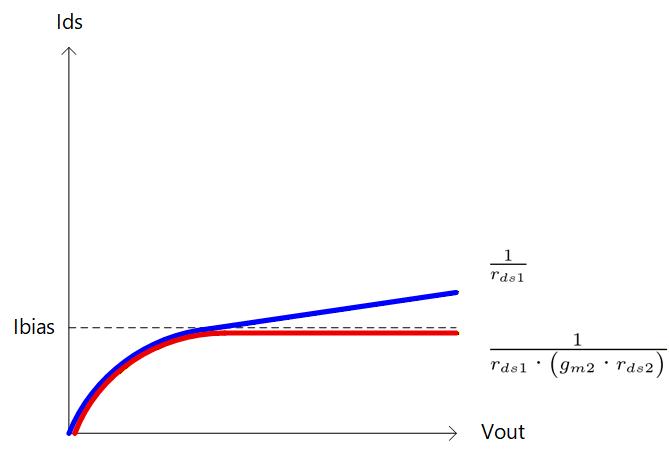
Fig. 5-2c
ここでは理想電流源に近づけることの意義については触れてきませんでしたが、オペアンプなどで非常に高いゲインを得るために、 をカスコード接続で “増幅” する場面が出てきます。
ミラー容量低減
先に述べたように、インバータはミラー容量を持つために高帯域化が難しいですが、カスコードを用いることで大幅に改善することが可能です。
ミラー容量は入力端子(Gate) と出力端子 (Drain) の間に があることで発生します。
このため、Fig. 5-3 のように出力端子と Drain の間にカスコードトランジスターを挿入して、出力端子と Drain を切り離すと、 がミラー容量に寄与しないようにでき、高帯域で動作させることが可能となります。
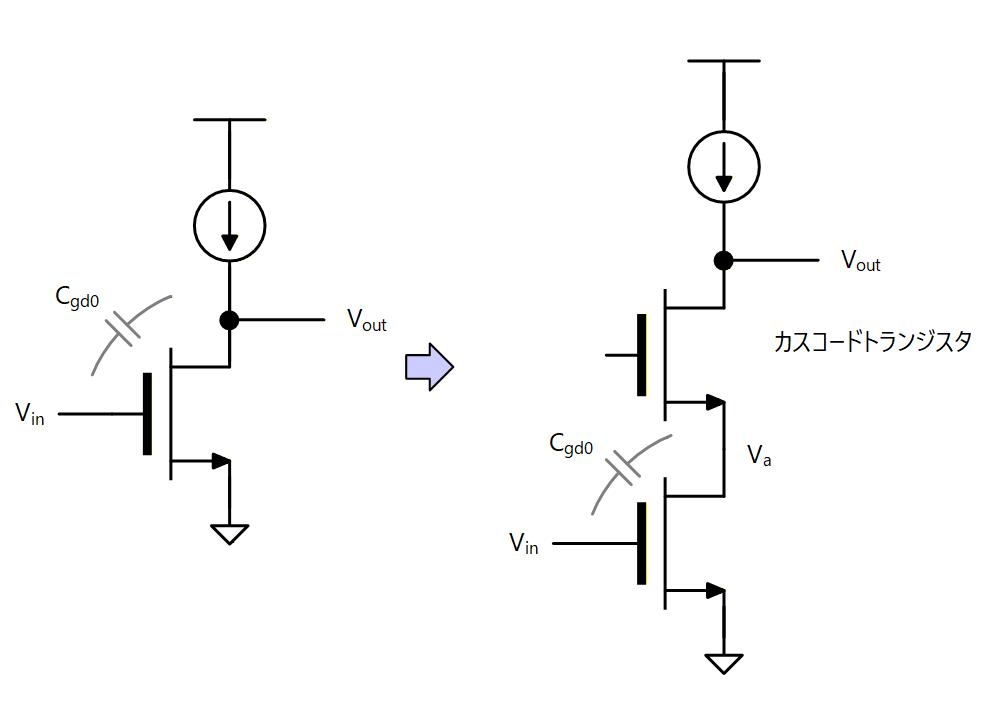
Fig. 5-3
まず、DC 的には電流源トランジスタの Gate には の電圧を与え、Drain 電圧は電流源トランジスタが 5極管動作するために必要な 電圧以上の を与えるようにカスコードトランジスタの Gate 電位を決めます。
つまり、 となるように を与えます。
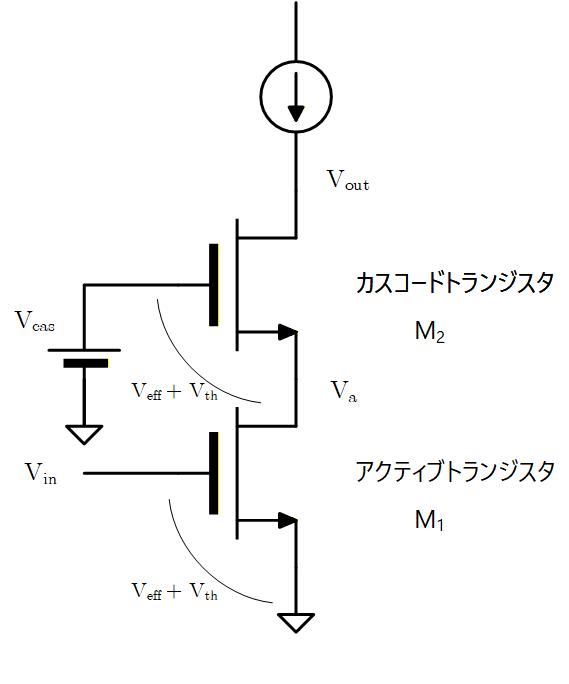
Fig. 5-4a
このバイアス条件で小信号解析を行います。
ここでは計算を簡単にするため、M1, M2 ともに 起因の小信号電流を無視します。
M1 は が変化するので に起因する小信号電流が流れます。
M2 は Gate 電圧は AC的に接地されているが、Source 電圧は変化するため、 に起因する小信号電流が流れ、これは M1 に流れる小信号電流 と等しいので、
以上から
よって に対する のゲインは
とすると、 に対する のゲインは -1 程度となり、ここでのミラー容量は と、カスコードトランジスタを入れない場合に対して大幅に改善することが可能になります。
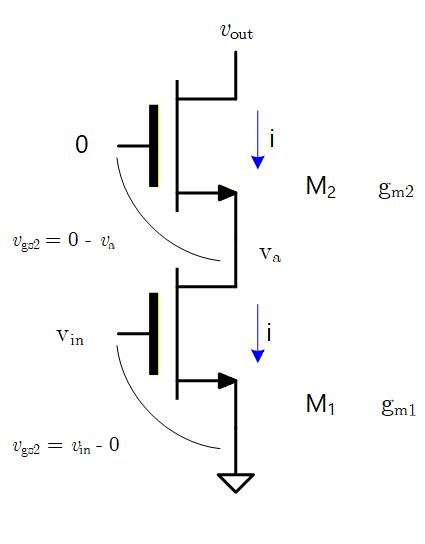
Fig. 5-4b
カスコードのデメリット
カスコードは非常に大きなメリットがありますが、デメリットもあります。
2つのトランジスタをそれぞれ 5極管領域で動作させないとカスコードの効果が得られません。
アクティブトランジスタの 5極管動作を保証するためには が条件となります。
いま を 0.2Vに設定したとして、マージンを 0.1V 程度みると 電圧は 0.3V 程度になります。
次にカスコードトランジスタの 5極管動作を保証するためには が条件となります。
今 を 0.2V にしたとすれば、 電圧を0.3V とすれば 電圧の下限は 0.5Vとなり、出力の電圧範囲はかなり狭くなります。
特に、電源電圧が低い微細化プロセスだと出力範囲が確保できないためカスコード接続が使えないケースも出てきます。
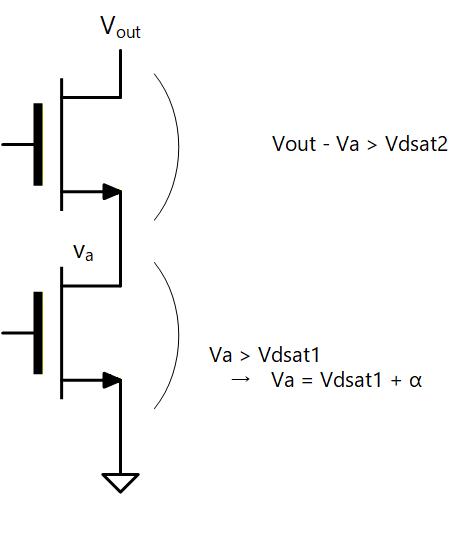
Fig. 5-5
プレーナプロセスでは を大きくすることは難しかったため、カスコードは非常に強力なツールでしたが、微細化が進み電源電圧が下がるにつれてだんだん使いにくくなってしまいました。
しかし、fin FET 時代に入ると、もともとの がプレーナトランジスタよりはるかに改善されたことから、無理にカスコードにしなくても何とかなる場合が増えたのは救いです。
差動対
差動対とは
Source を共通にした 2つのトランジスタを差動対と呼びます。
さらにその共通の Source とグラウンドの間に定電流源を挿入した形の回路を、電流源 Tail の差動対と呼びます。
定電流源の代わりに抵抗を入れたものを抵抗 Tail の差動対と呼びます。
また、共通の Source を直接グラウンドに接続したものを Non-Tailと呼ぶこともあります。
一般には電流源 Tail の差動対が使われます。
動作としては、POS 側トランジスタに流れる電流 と、NEG 側トランジスタに流れる電流 の和が電流源 に流れるため、POS 側と NEG 側で電流の取り合いをすることになります。
2つのトランジスタの Source が共通なので、 であれば POS 側の が NEG 側の より高くなるため、 となり、 であれば となります。
つまり差動対は と の電圧差を と の電流差に変換する回路であると言えます。
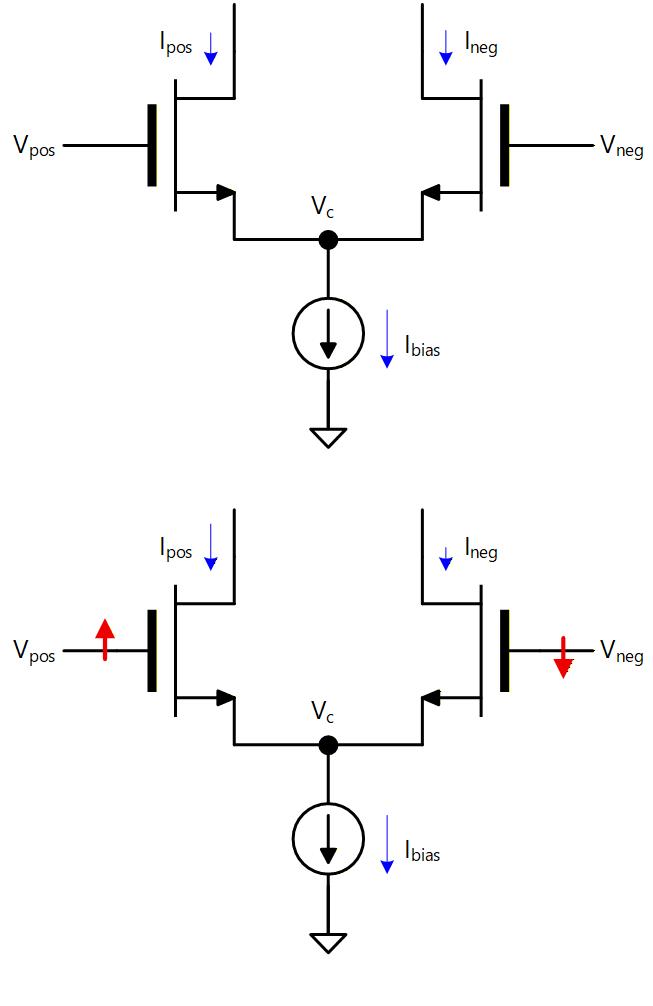
Fig. 6-1
抵抗負荷の差動インバータ
続いて、差動対に負荷として抵抗を接続した場合を考えます。
POS 側のトランジスタの Gate, Drain 端子入力をそれぞれ
とし、流れる電流を とします。
同様に、NEG 側について、それぞれ を定義します。
ここで、 の場合には となって、
となります。
次に の場合には、先に述べたように となり、POS 側の方がより電位降下が大きくなるため となります。
これまでは POS 側、NEG 側の入出力電圧を個別に書いてきましたが、差動対を扱う場合には以下のように「差動電圧」と 「同相電圧」で表すのが一般的です。
差動電圧 は POS側とNEG側の差電圧で、同相電圧 は POS側とNEG側の中点電圧になります。
同相電圧は動作点電圧とも呼ばれます。
これらの式を変形すると
と はそれぞれ動作点 を基準として づつ上下に振れると見ることもできます。
アナロジーとしてはシーソーのように考えるとわかりやすいかと思います。
つまり支点(動作点) を真ん中にして、一方が上がれば同じ分だけ反対側が下がるというイメージになります。
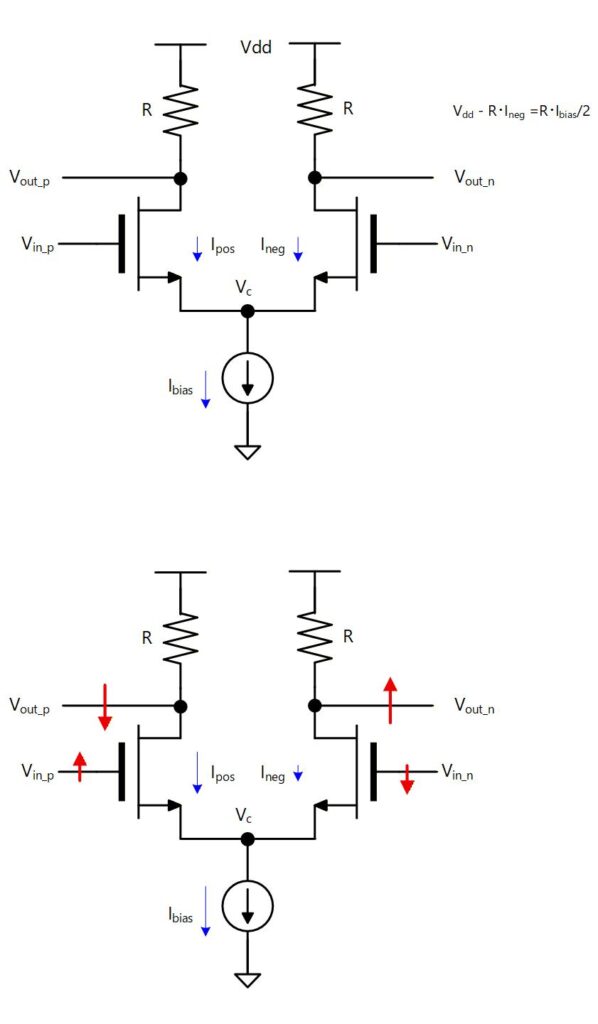
Fig. 6-2
右図上の抵抗負荷の差動対を小信号等価回路で書くと右図下のように書けます。
(小信号なので記号は全て小文字で書いています)
まず、電源電圧は動かないので接地になります。また、定電流源も変化はないので小信号電流はゼロです。
トランジスタは本来 がありますが、 に比べて電流に対する寄与が圧倒的に小さいため無視します。
POS 側、NEG 側のトランジスタについて小信号電流はそれぞれ
ここで、2式の差を取ると
で、 とすると
ここで なので から、
この は負荷抵抗に流れてそれぞれ電位降下を起こし
両式の各辺同士の差を取ると
なので、結局
となって通常のインバータと同じゲインの差動インバータができることになります。(Fig. 6-4)
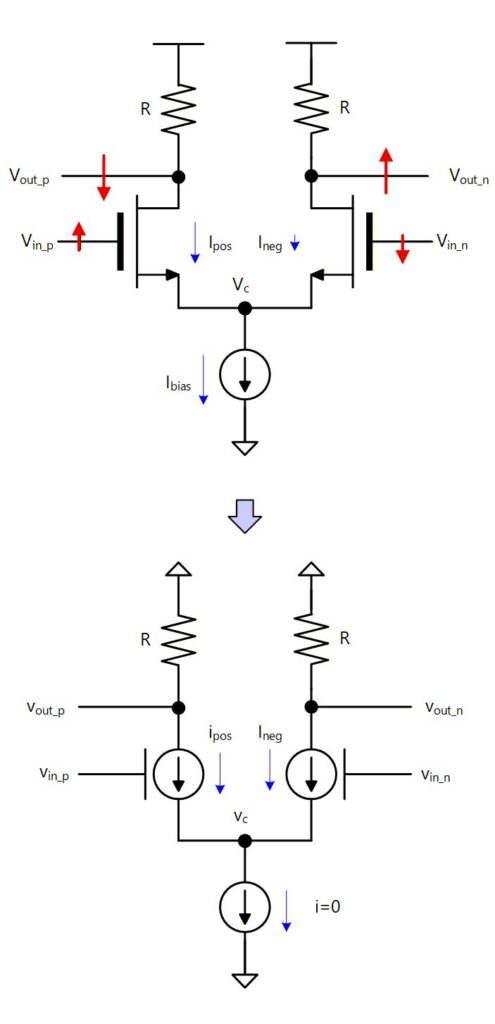
Fig. 6-3
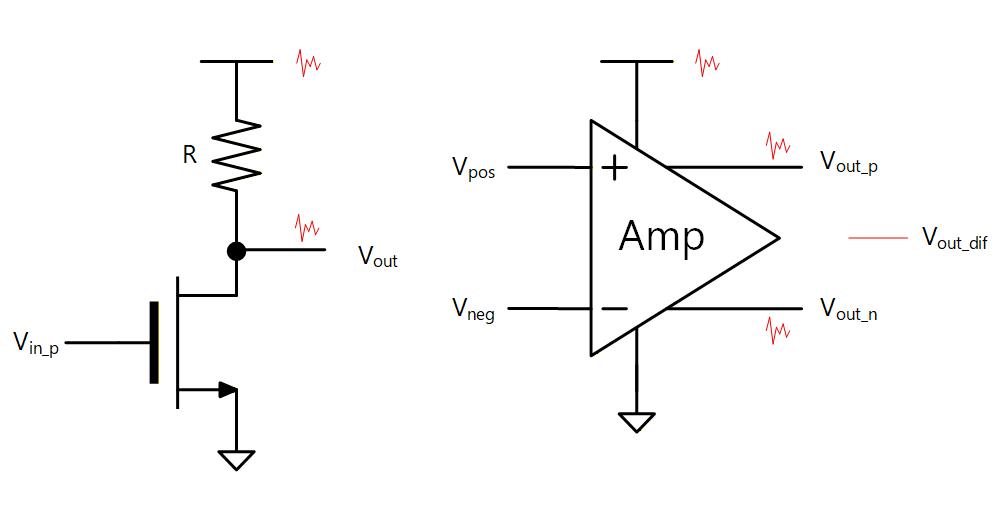
Fig. 6-4
差動インバータの利点の1つに、電源ノイズ耐性が優れていることがあげられます。 シングルエンドの場合は、 に電源ノイズが重畳されると、その影響が出力に及びます。 しかし差動にした場合には POS 側と NEG 側を個別にみると確かに電源ノイズの影響は受けますが、両方に等しくノイズが乗るために、差を取るとそのノイズがお互いにキャンセルして、差動出力としてはノイズは乗りません。 なので、特に微小電圧を扱う回路では差動で回路を構成することがよくあります。
同相特性と CMRR
これまでは差動入力に対する特性をみてきましたが、今度は同相入力に対する特性を考えます。
同相特性というのは、 と を同相で動かしたときの特性で、 として、 を変化させたときの の応答になります。
このときの回路は Fug. 6-5 上図の回路を真ん中で折りたたみ、POS 側と NEG 側を重ねたものと等価になりますので、Fig. 6-6 下図のように、ソースフォロワーの Drain と の間に抵抗を挿入したような回路になります。
入力の Gate 電圧を変化させると Source 電圧もそれに連動して変化しますが、電流源が理想定電流源なら 電圧が変わっても抵抗に流れる電流は変わらないため、 の電圧は変わりません。
すなわち、同相入力に対する同相出力はゲインを持ちません。
ただ、実際には電流源はトランジスタで作るため、理想定電流源にはなりません。 具体的にはトランジスタの がみえてくることになります。
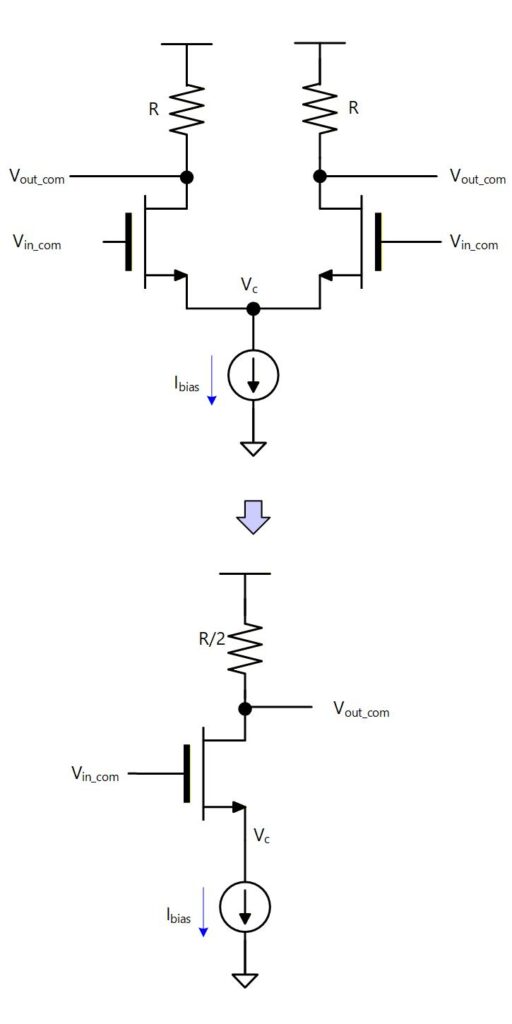
Fig. 6-5
こらを小信号等価回路で考えます。
電源電圧は変化しないため接地となり、電流源のトランジスタは Gate 電圧固定で使うため、 による電流変化はなく、値が となる抵抗としてのみ働きます。
トランジスタの方は の効果を無視すると だけが電流変化に寄与し、 すなわち と の電位差に応じて電流が変わります。
すなわち、トランジスタを流れる小信号電流は
この小信号電流が電流源にそのまま流れるので、
したがって
とすると
小信号電流は
この小信号電流が負荷抵抗に流れるため
したがって
を数100kΩ、 を数kΩ程度とするとこの同相ゲインは 1/100 程度と、差動ゲインよりも非常に小さい値を取ります。
差動ゲインと同相ゲインの比を CMRR (common Mode Reduction Ratio) と呼び、差動インバータの特性指標として用いられます。
この値は大きい方が、すなわち差動ゲインはなるべく大きく、同相ゲインはなるべく小さくするのが望ましいです。
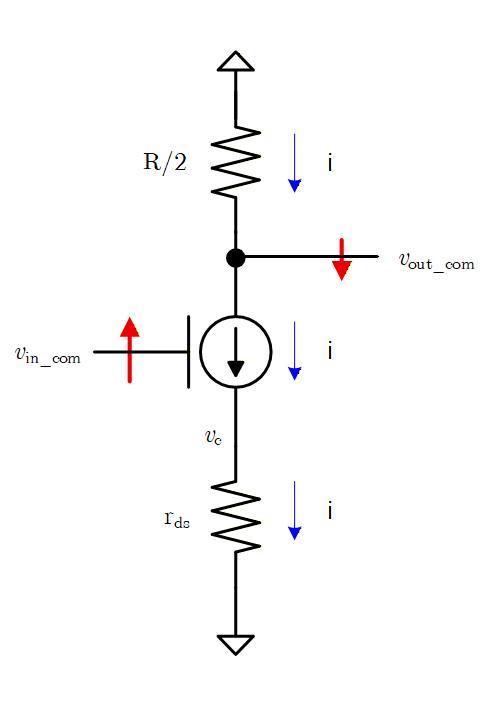
Fig. 6-6
シングルエンド出力
これまでは入力も出力も差動の、差動入力インバータについて見てきましたが、入力は差動でも出力はシングルエンドのいわゆる差動アンプについて説明します。
代表的な回路図を Fig. 6-7 に示しますが、これまで抵抗負荷だった個所が PMOS カレントミラーに置き換わったような形になります。
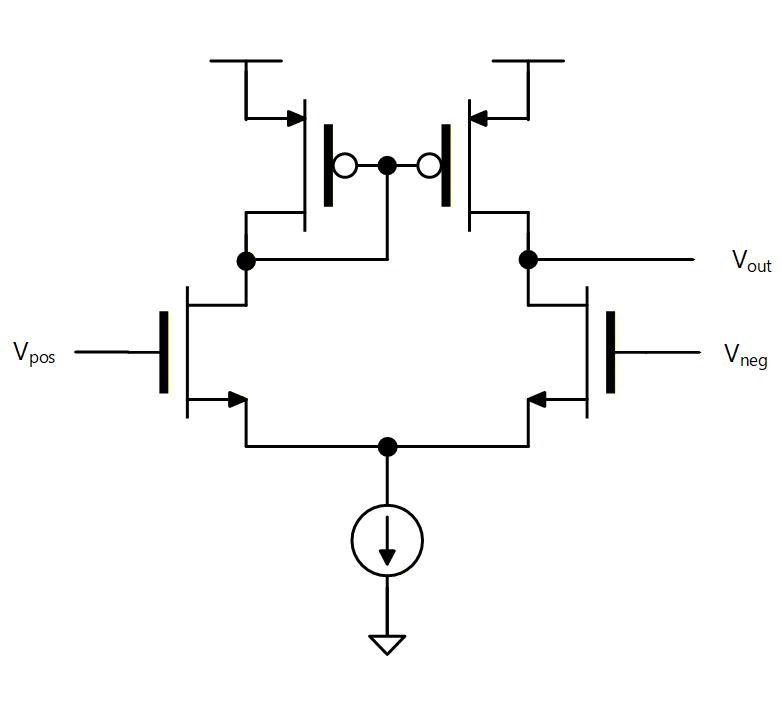
Fig. 6-7
まず、 電圧だけが高くなった場合を考えます。
電圧が高くなると POS 側の NMOSトランジスタに流れる電流が増えます。 その電流は PMOS トランジスタにもそのまま流れ、それがカレントミラーで NEG 側の PMOS に折り返され、 ノードは流れ込む電流により電位が上がることになります。 この電流は から見える大きな出力抵抗によって電圧に変換されるため、 を正相で増幅することになります。
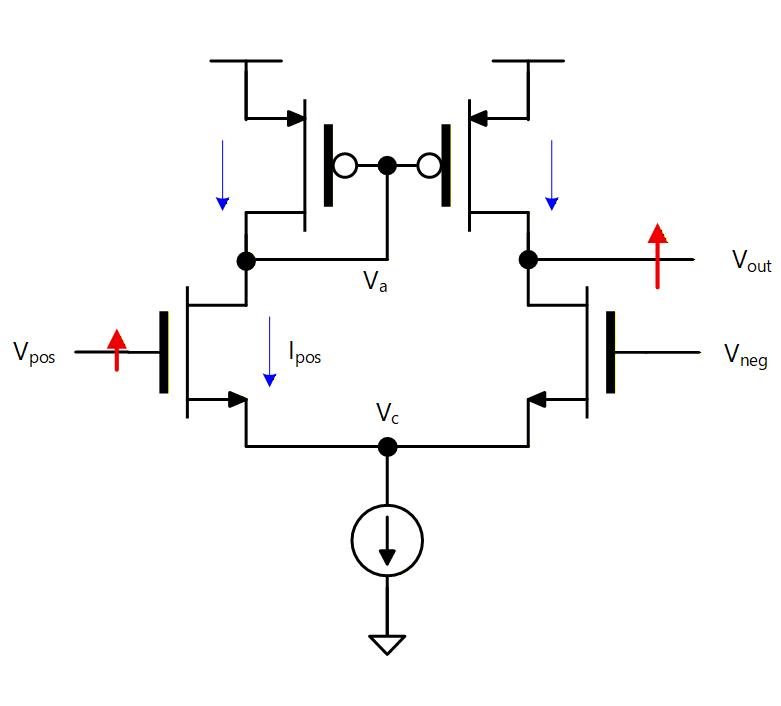
Fig. 6-8a
次に、 電圧だけが高くなった場合を考えます。
電圧が高くなると NEG 側の NMOSトランジスタに流れる電流が増えます。 その電流は、 ノードから流出するため 電位は下がることになります。
この電流は から見える大きな出力抵抗によって電圧に変換されるため、 は逆相で増幅されることになります。
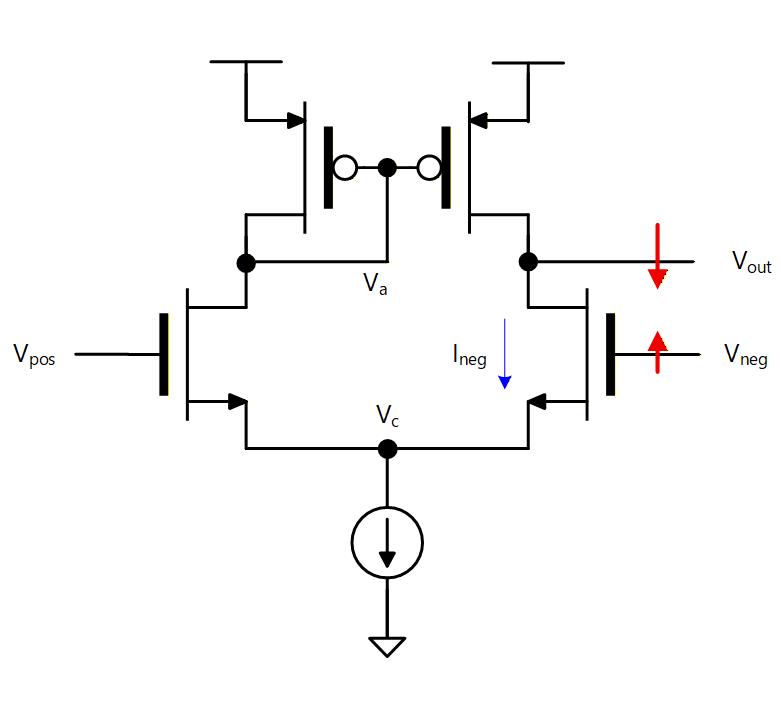
Fig. 6-8b
Fig. 6-9 にこの様子を示します。
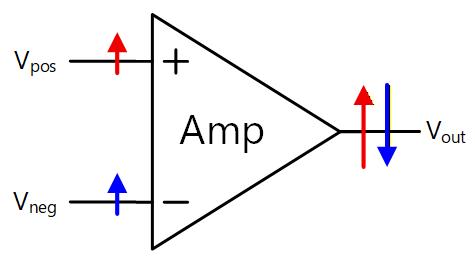
Fig. 6-9
続いて、小信号解析を行ってゲインを定量的に求めます。
Fig. 6-10 の回路図で、電流源は定電流源とみて小信号的にはないものとします。
M1, M2 については を無視して のみを考え、M3, M4 については , とおきます。
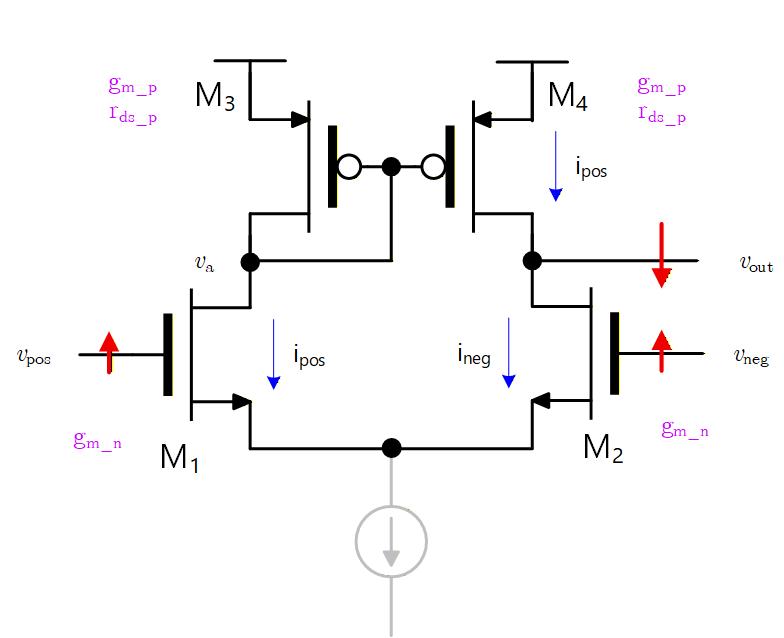
Fig. 6-10
M1, M2 のトランジスタについて
両辺をそれぞれ引くと、 として
また定電流源の を無視すると iとなるから
M3 のトランジスタについては M1 と同じ小信号電流が流れるから
ここで負号がついているのは M3 が PMOS のため極性が逆になるためです。
これを について解くと
M4 のトランジスタについて流れる電流はM2 と等しいので
なので を無視すると
だから
以上から
となり、ここでも と の積が入出力ゲインになることがわかります。
なお、M1, M2 の を無視せずに としたときには
となります。
は数100kΩ〜数MΩで、 は数mMho なので、ゲインは 20〜30dB と抵抗負荷の差動対に比べるとはるかに大きいゲインが得らることがわかります。
これだけでもちょっとしたオペアンプとして使えそうですが、まだゲインが足りません。 本格的なオペアンプを作る場合は、後段にインバータを追加するなどして、最終的に 40dB〜60dB という高いゲインを稼ぐ必要があります。
詳細はオペアンプの章で解説します。
まとめ
以上、アナログ回路でよく用いる基本的なパーツの説明をしてきました。 一見して複雑に見える回路でも、機能ごとに腑分けしていくと多くの場合はこれまで説明してきた回路要素に帰着させることができます。 この腑分けができるようになると、他人が書いた回路図でもその中身が容易に把握できるようになりますし、自分で回路を設計する場合にも論理的に回路を組み立てることが可能になると思います。



コメント